Аксіоми стереометрії. Паралельність прямих і площин у просторі

1. Площина

Уявлення про площину дають нам, наприклад, поверхня столу, віконного скла, спокійного озера. Площина, як і пряма, нескінченна. Площина не має «країв», вона є необмеженою фігурою.

На малюнках площину зображають у вигляді паралелограма або у вигляді довільної області.

                  

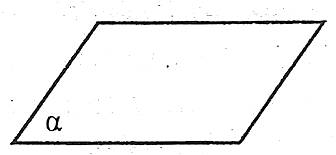
Площини позначають маленькими грецькими літерами: α, β, γ,…

Розділ геометрії, у якому вивчаються властивості фігур у просторі, називається стереометрією.

Основними фігурами у просторі є точки, прямі, площини.

Аксіоми стереометрії

1. Якою б не була площина, існують точки, що їй належать, й точки, які не належать їй.

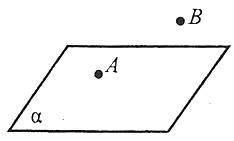
Наприклад: точка А лежить у площині α (або належить площині α), а точка В знаходиться поза площиною α (або не належить площині α). Коротко це записується так:  .

Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, яка проходить через цю точку.

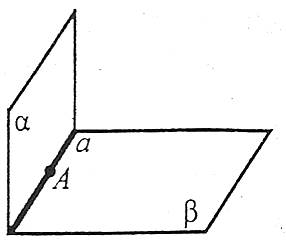
Якщо дві різні площини мають спільні точки, то кажуть, що вони перетинаються.

Якщо дві різні прямі мають спільну точку, то через них можна провести площину, і до того ж тільки одну.

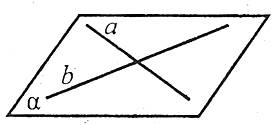
Наслідки з аксіом стереометрії

Теорема про існування і єдність площини, яка проходить через дану пряму і дану точку

Через пряму і точку поза нею можна провести площину, і до того ж тільки одну.

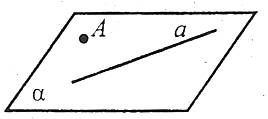
Теорема про існування і єдність площини, яка проходить через три точки

Через три точки, які не лежать на одній прямій, можна провести площину, і до того ж тільки одну.

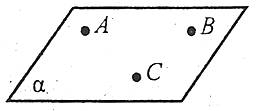
Якщо точки А, В, С не лежать на одній прямій, то площину, яка містить ці точки, позначають так: (АВС).

Теорема про належність прямої площині

Якщо дві точки прямої належать площині, то й уся пряма міститься в цій площині.

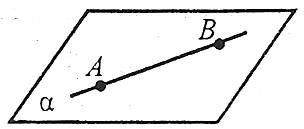
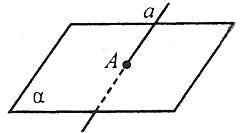
Із цієї теореми випливає, що пряма а може лежати в площині, а може і не належати площині α. Якщо пряма і площина мають лише одну спільну точку, то кажуть, що вони перетинаються.