Аксіоми стереометрії. Паралельність прямих і площин у просторі

2. Паралельність прямої і площини

     Дві прямі у просторі називаються паралельними, якщо вони лежать в одній площині та не перетинаються.

    Наприклад: а та b паралельні. Паралельність прямих а та b позначається так: .

    Теорема про існування єдиної прямої, паралельної даній прямій

     Через точку, яка не лежить на прямій, можна провести пряму, паралельну цій прямій, до того ж тільки одну.

    Ознака паралельності прямих

     Дві прямі, паралельній третій прямій, паралельні, якщо , то .

     Дві прямі називають мимобіжними, якщо вони не лежать в одній площині.

    Наприклад: а і b мимобіжні.

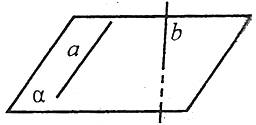
    Ознака мимобіжності прямих

     Якщо одна із двох прямих лежить у деякій площині, а друга пряма перетинає цю площину в точці, яка не лежить на першій прямій, то ці прямі мимобіжні.

     Пряма та площина називаються паралельними,якщо вони не мають спільних точок.

    Наприклад: пряма а та площина α паралельні. Паралельність прямої а та площини α позначається так: .

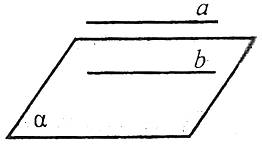
    Ознака паралельності прямої та площини

     Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині. Якщо .