Конуси та їх властивості

Конуси та їх властивості

1. Конус.

Конусом називається тіло, утворене обертанням прямокутного трикутника навколо одного із катетів.

Якщо прямокутний трикутник SAO обертається навколо катета SO, то його гіпотенуза SA, описує бічну поверхню, а катет ОА – круг – основу конуса.

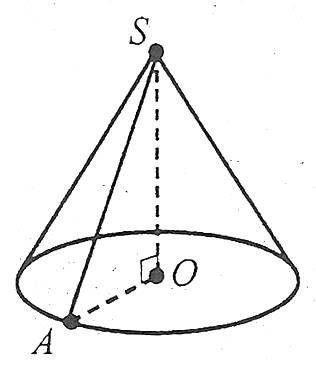
Радіус цього круга називається радіусом конуса; точка S, відрізок SA, відрізок SO, пряма SO називаються відповідно вершиною, твірною, висотою і віссю конуса.

2. Перерізи конуса.

Осьовий переріз конуса – переріз конуса площиною, яка проходить через його вісь. Усі осьові перерізи конуса є рівнобедреними трикутниками, рівними між собою.

Наприклад:  – осьовий переріз (SA=SB).

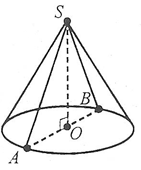
Переріз конуса площиною, яка паралельна площині основи конуса, є круг.

Зрізаним конусом називається частина конуса, обмежена його основою і перерізом, паралельним площині основи.

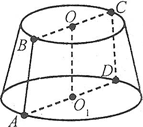
Зрізаний конус можна одержати в результаті рівнобедреної трапеції навколо її осі симетрії або обертаючи прямокутну трапецію навколо осі, що збігається з бічною стороною трапеції, перпендикулярною до основ.

Осьовий переріз зрізаного конуса – рівнобічна трапеція.

Наприклад: ABDC – осьовий переріз.

Зрізаний конус обмежений двома кругами – його основами – і бічною поверхнею.

Відстань між основами – висота зрізаного конуса.

Наприклад: ОО1 – висота, АВ – твірна.

Примітка. Якщо точніше, то тіло, утворене обертанням прямокутного трикутника навколо одного із катетів, називається прямим круговим конусом. Саме такі конуси розглядають у шкільному курсі стереометрії і називають їх просто конусами. У широкому розумінні слова, конус – це тіло, утворене всіма відрізками, які з’єднують дану точку (вершину конуса) з точками деякої обмеженої плоскої фігури (основою конуса).