Декартові координати у просторі
4. Рівняння фігури
Рівнянням фігури в декартових координатах у просторі називається рівняння із трьома невідомими х, у, z, які задовольняють координати будь-якої точки фігури, і тільки вони.
Рівняння сфери
Якщо в просторі задано деяку точку з координатами С(а,b,c), що є центром сфери, а також радіус R, то рівняння сфери має вигляд
![]() .
.
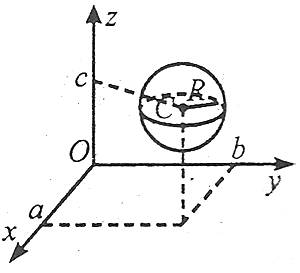
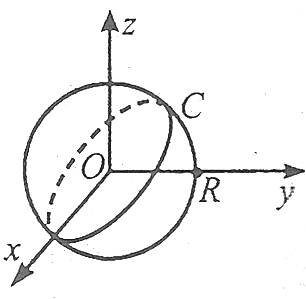
Якщо центром сфери є початок координат, то маємо
![]() .
.
Приклад 4. Складіть рівняння сфери з центром в точці В(1;1;3), якщо відомо, що сфера проходить через точку М(2;0;-1).
Розв’язання
Знайдемо радіус R сфери
![]() .
.
Ураховуючи, що центр сфери міститься в точці В(1;1;3), а радіус R сфери дорівнює ![]() , матимемо рівняння сфери
, матимемо рівняння сфери
![]() .
.
Відповідь: ![]() .
.