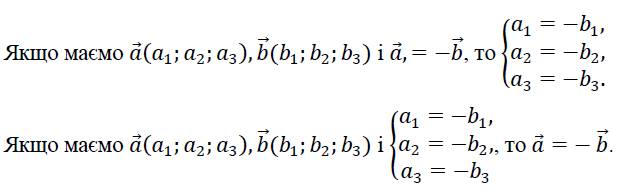Вектори у просторі
1. Координати вектора. Довжина вектора
1. Координати вектора
Координати вектора ![]() , що має початок в точці А і кінець в точці В, дорівнюють різниці відповідних координат точок В і А.
, що має початок в точці А і кінець в точці В, дорівнюють різниці відповідних координат точок В і А.
Координати вектора у просторі
Якщо початком вектора є точка А(хА;уА;zA), а кінцем – точка В(хВ;уВ;zB), то
![]()
2. Довжина вектора
Довжина вектора (абсолютна величина, або модуль) – довжина відрізка, що зображує вектор. Позначення: ![]() .
.
Довжина вектора у просторі
Якщо є вектор![]() , то
, то![]() =
= ![]() , де
, де ![]() – модуль вектора,
– модуль вектора, ![]() – його координати.
– його координати.
Одиничним називається вектор ![]() , у якого
, у якого ![]() .
.
Нульовим називається вектор![]() \, у якого початок і кінець збігаються. Нульовий вектор не має визначеного напрямку, а його модуль дорівнює нулю.
\, у якого початок і кінець збігаються. Нульовий вектор не має визначеного напрямку, а його модуль дорівнює нулю.
Задача 1. Знайдіть координати і довжини векторів ![]() і
і![]() , якщо А(2;-3;-1), В(-4;-8;5), С(3;1;-2).
, якщо А(2;-3;-1), В(-4;-8;5), С(3;1;-2).
Розв’язання
![]() ( - 4 - 2; - 8 - ( - 3);5 - ( - 1)) =
( - 4 - 2; - 8 - ( - 3);5 - ( - 1)) = ![]() ( - 6; - 5;6)\];
( - 6; - 5;6)\];
![]() (3 - 2;1 - ( - 3); - 2 - ( - 1)) =
(3 - 2;1 - ( - 3); - 2 - ( - 1)) = ![]() (1;4; - 1)\];
(1;4; - 1)\];
![]() =
= ![]() ;
;
![]() =
= ![]() .
.
Відповідь:![]() ,
, ![]() ,
,![]() \,
\, ![]() .
.
Рівність векторів у просторі
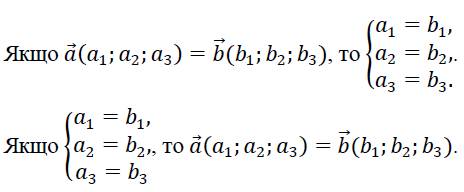
Протилежні вектори у просторі