НАТУРАЛЬНІ ЧИСЛА ТА ДІЇ НАД НИМИ
Короткий виклад теоретичного матеріалу з теми "Натуральні числа та дії над ними".
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | НАТУРАЛЬНІ ЧИСЛА ТА ДІЇ НАД НИМИ |
| Надруковано: | Гість |
| Дата: | Wednesday 2 July 2025 4:41 AM |
1. Натуральні числа
Натуральні числа ― це числа, що використовуються для лічби: 1, 2, 3, …, n, … . Множину натуральних чисел позначають символом ℕ. ℕ = {1, 2, 3, …}.
Будь-яке натуральне число n у десятковій системі числення можна подати у вигляді
![]()
де ![]() можуть набувати значення 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а число
можуть набувати значення 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а число ![]() ― значення 1, 2, 3, 4, 5, 6, 7, 8, 9.
― значення 1, 2, 3, 4, 5, 6, 7, 8, 9.
Позиційний запис цього числа має вигляд
![]() .
.
Наприклад:
![]() ;
;
![]() .
.
2. Порівняння натуральних чисел
Із двох натуральних чисел більшим (меншим) є те число, яке при лічбі з’являється пізніше (раніше).
Наприклад: 17 < 20; 129 > 120.
Найменшим натуральним числом є 1. Найбільшого натурального числа не існує.
Із двох натуральних чисел із різною кількістю цифр більшим є те, яке позначене більшою кількістю цифр. Якщо два натуральних числа мають однакову кількість цифр, то більшим є те число, в якому більше одиниць у найвищому розряді. Якщо кількість одиниць у цьому розряді однакова, то порівнюються розряди, що на ступінь нижче і т.д.
Наприклад: 10256 > 989; 10256 < 10356.
Правила запам'ятовування знаків «>» і «<»
- Подумки провести риску через нижню частину знака « >» або « <». У першому випадку дістанемо знак, подібний до числа 7, а в другому — до числа 4. Оскільки 7 >4, то знак « >» означає «більше», а знак « <» — «менше».
- Знаки « >» і « <» подібні до стріл, «якими більше число заколює
менше».
3. Округлення натуральних чисел
Щоб округлити натуральне число до певного розряду, треба:
1) замінити нулями всі цифри, що стоять після цього розряду;
2) якщо наступна за цим розрядом цифра була 5, 6, 7, 8 або 9, то цифру розряду, до якого виконується округлення, збільшити на одиницю;
3) якщо наступна за цим розрядом цифра була 0, 1, 2, 3 або 4, то цифру розряду, до якого виконується округлення, залишити без змін.
Наприклад: числа 125 128, 59 393 округлені до десятків, до сотень відповід-но дорівнюють 125 130, 59 390 і 125 100, 59 400, тобто 125 128 ≈ 125 130, 59 393 ≈ ≈ 59 390, 125 128 ≈ 125 100, 59 393 ≈ 59 400.
Нагадаємо розряди натурального числа: сотні мільярдів, десятки мільярдів, одиниці мільярдів, сотні мільйонів, десятки мільйонів, одиниці мільйонів, сотні тисяч, десятки тисяч, одиниці тисяч, сотні, десяті, одиниці.
4. Дії над натуральними числами
Додавання натуральних чисел
![]()
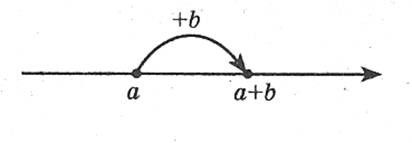
![]()
Наприклад: 5 + 3 = 5 + 1 + 1 + 1 = 8.
Додавання багатоцифрових натуральних чисел виконується порозрядно (додавання одноцифрових чисел кожного стовпчика, починаючи з правого стовпчика).
Наприклад:
362 + 473 = 835;
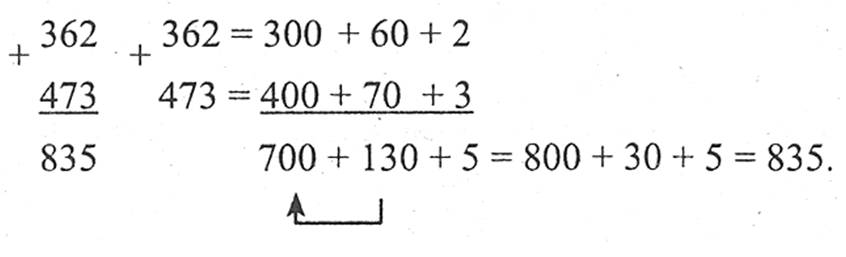
Віднімання натуральних чисел
![]()
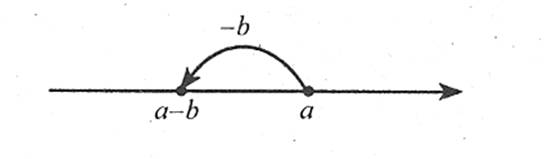
Відняти від числа a число b означає знайти таке число с, що a = b + с.
![]()
Наприклад: 10 – 3 = 10 – 1 – 1 – 1 = 7.
Віднімання багатоцифрових натуральних чисел виконується порозрядно (віднімання одноцифрових чисел кожного стовпчика, починаючи з правого стовпчика).
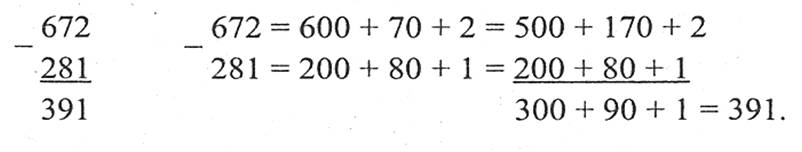
Множення натуральних чисел
![]()
![]()
Наприклад: 2 ˑ 3 = 2 + 2 + 2 = 6.
Множення багатоцифрових натуральних чисел виконується «у стовпчик».
Наприклад: 459ˑ275=126225.
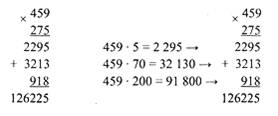
Ділення натуральних чисел
![]()
Розділити число a на число b означає знайти таке число с, що a = b ˑ с.
Натуральне число a розділити на натуральне число b означає підрахувати, скільки разів треба відняти число b від числа a, щоб одержати нуль.
Наприклад: 6 : 3 = 2, бо 6 – 3 – 3 = 0.
Ділення натуральних чисел з остачею
Якщо a ― ділене, b ― дільник і a = bс + r, де b > r, то говорять, що при діленні числа a на число b маємо неповну частку с та остачу r:
![]() .
.
Наприклад: 10 : 4 = 2 (остача 2), 10 = 4 · 2 + 2.
Ділення багатоцифрових чисел виконується «кутом».
Наприклад:
113 сотень: 28 = 4 сотні (остача 1 сотня);
19 десятків: 28 = 0 десятків (остача 19 десятків);
196 : 28 = 7.
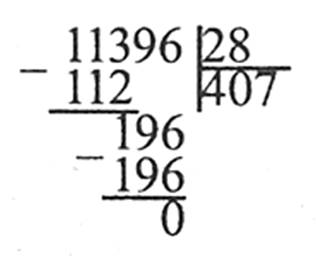
5. Подільність натуральних чисел
Натуральне число a ділиться на натуральне число b націло ![]() , якщо існує натуральне число с таке, що a = b · с.
, якщо існує натуральне число с таке, що a = b · с.
Наприклад: ![]() .
.
Якщо ![]() , то b ― дільник a, a ― кратне b.
, то b ― дільник a, a ― кратне b.
Властивості подільності:
Якщо ![]() .
.
Якщо ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() .
.
Якщо ![]() , то
, то ![]() .
.
6. Ознаки подільності натуральних чисел
На 2: Натуральне число ділиться на 2 тоді і тільки тоді, коли його остання цифра ділиться на 2.
На 3: Натуральне число ділиться на 3 тоді і тільки тоді, коли сума його цифр ділиться на 3.
На 4: Натуральне число ділиться на 4, якщо дві його останні цифри утворюють число, що ділиться на 4, або дві його останні цифри ― нулі.
На 5: Натуральне число ділиться на 5 тоді і тільки тоді, коли його остання цифра або 0, або 5.
На 6: Натуральне число ділиться на 6 тоді і тільки тоді, коли воно ділиться на 2 і на 3.
На 8: Число ділиться на 8 тоді і тільки тоді, коли число, утворене його трьома останніми цифрами ділиться на 8.
На 9: Натуральне число ділиться на 9 тоді і тільки тоді, коли сума його цифр ділиться на 9.
На 10: Натуральне число ділиться на 10 тоді і тільки тоді, коли його остання цифра 0.
7. НСД, НСК, взаємно прості, прості та складені числа
Найбільшим спільним дільником чисел a і b називається найбільше число, на яке ділиться і число a, і число b. Позначення ― НСД (a;b).
Наприклад: НСД (5;15) = 5, НСД (15; 9) = 3.
Найменшим спільним кратним чисел a і b називається найменше число, на яке ділиться і число a, і число b. Позначення ― НСК (a; b).
Наприклад: НСК (5; 15) = 15, НСД (15; 9) = 45.
НСК (a; b)·НСД (a; b) = a · b.
Числа a і b називаються взаємно простими, якщо НСД (a; b) = 1.
Наприклад: числа 3 і 5 взаємно прості, бо НСД (3; 5) = 1.
Прості числа ― натуральні числа, які мають рівно два різних дільники (одиницю і саме число).
Наприклад: 2; 3; 5; 7; 11; 13;… ― прості числа.
Складені числа ― натуральні числа, які мають більше двох дільників.
Наприклад: 4; 6; 9; 10;… ― складені числа.
Будь-яке складене число n можна розкласти на прості множники, тобто подати його у вигляді
![]() ,
,
де ![]() ― прості числа, а
― прості числа, а ![]() ― натуральні числа.
― натуральні числа.
Наприклад: ![]() .
.