ПОЧАТКОВІ ПОНЯТТЯ ПЛАНІМЕТРІЇ
Початкові поняття планіметрії
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Геометрія. |
| Книга: | ПОЧАТКОВІ ПОНЯТТЯ ПЛАНІМЕТРІЇ |
| Надруковано: | Гість |
| Дата: | Saturday 24 May 2025 9:00 PM |
1. Початкові поняття
Геометрія – це наука, яка вивчає властивості геометричних фігур. Прикладами геометричних фігур є трикутник, коло, квадрат. Розділ геометрії, в якому вивчаються властивості фігур на площині, називається планіметрією.

Точка і пряма є основними геометричними фігурами на площині.
Точка не має розмірів. Уявлення про точку дає слід кінчика олівця на папері. Точки позначаються великими латинськими літерами A, B,C,…
Уявлення про пряму дає натягнута нитка. Пряма нескінченна. Прямі позначають або однією латинською літерою: a, b, c,…, або двома великими латинськими літерами, які лежать на прямій: AB, BC,…
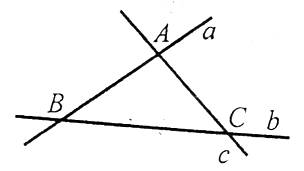
Частина прямої, обмежена двома точками, називається відрізком. Точки, які обмежують відрізок, називають його кінцями.
Наприклад: відрізок із кінцями в точках А і В. Такий відрізок позначають АВ або ВА.

Променем, або півпрямою, називається частина прямої обмежена з однієї сторони точкою. На рис. точка О називається початком променя. Промінь позначають або однією латинською літерою (промінь l), або двома великими латинськими літерами, перша із яких позначає початок променя, а друга – довільну точку на промені (промінь ОА).

Точка О, яка лежить на прямій, поділяє її на два промені, напрями яких протилежні. Ці промені називають доповнювальними.
![]()
2. Геометрична фігура
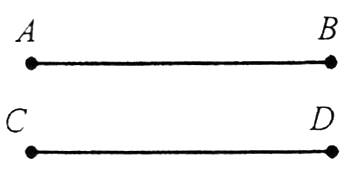
Геометричною фігурою називається будь-яке утворення з точок. Геометричні фігури називаються рівними, якщо вони збігаються при накладанні. На рис. зображено рівні відрізки AB і CD. Це записується так: AB=CD.
Найпростішою геометричною фігурою є точка. З точок складаються всі інші геометричні фігури.
Отже,будь яка множина точок є геометричною фігурою.
Частина геометричної фігури теж є геометричною фігурою.
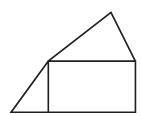
Геометричною фігурою є й об’єднання кількох геометричних фігур. На рис. фігура складається з прямокутника та двох трикутників.
Однією з основних геометричних фігур є площина. Уявлення про частину площини дає поверхня стола, шибки, стелі.
Основними геометричними фігурами на площині є точка і пряма.
3. Поняття про аксіоми та теореми
Геометрія вивчає властивості фігур, які виражаються різними твердженнями: означеннями, аксіомами, теоремами.
Означення – це твердження, яке пояснює дане поняття через уже відомі поняття.
Аксіома – це твердження, яке приймається на віру (без доведення).
Наприклад:
1. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй.
2. Через будь-які дві точки можна провести пряму, і тільки одну.
![]()
3. Пряма розбиває площину на дві півплощини.
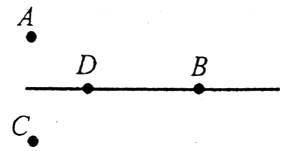
4. Із трьох точок прямої одна і тільки одна лежить між двома іншими.
![]()
Теоремою називається твердження про властивість фігури, істинність якого встановлюється у результаті міркувань. Ці міркування називаються доведенням.
Наведемо приклад.
Теорема. Дві різні прямі можуть перетинатися тільки в одній точці.
Доведення
Якби дві різні прямі мали дві точки перетину, то через ці точки проходили б дві різні прямі. А це неможливо, оскільки через дві різні точки можна провести тільки одну пряму (аксіома 2). Отже, дві різні прямі не можуть мати дві різні точки перетину.
4. Поняття про обернену теорему
Будь-яка теорема складається із двох частин: перша частина – умова (тобто те, що задано), друга частина – висновок (тобто те, що треба довести).
Приклад. Якщо дві різні прямі перетинаються (умова), то вони мають лише одну спільну точку (висновок).
Якщо поміняти місцями висновок і умову в теоремі, то о держимо теорему, обернену до даної. Дану теорему називають прямою.
Наприклад: теорема «Якщо дві різні прямі мають спільну точку (умова), то вони перетинаються (висновок)» є оберненою до теореми «Якщо дві різні прямі перетинаються (умова), то вони мають лише одну спільну точку (висновок)».
Слід зазначити, що з істинності прямої теореми не завжди випливає справедливість (істинність) оберненого твердження.
5. Довжина відрізка та її властивості
Основні властивості вимірювання відрізків виражаються аксіомами.
Аксіома вимірювання відрізків
Кожний відрізок має певне довжину, більшу за нуль. Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою точкою, тобто якщо С – точка відрізка АВ, то АВ=АС+ВС.
![]()
Знаходження довжини відрізка засноване не порівнянні його з деяким відрізком, який приймається за одиницю вимірювання. Вибравши одиницю вимірювання, можна знайти довжину будь-якого відрізка. На практиці для вимірювання довжин відрізків частіше за все використовують міліметр, сантиметр, дециметр, метр, кілометр. Ці одиниці вимірювання довжин пов’язані між собою, зокрема, 1 км=1000 м, 1 м=100 см, 1 дм=10 см, 1 см=10 мм.
Рівні відрізки мають однакову довжину і навпаки: якщо відрізки мають однакову довжину, то вони рівні.
Серединою відрізка називається точка цього відрізка, яка ділить його навпіл (тобто на два рівних відрізки).
Точка С – середина відрізка АВ,оскільки АС=СВ (рівні відрізки на малюнках познають однаковою кількістю рисок).
![]()
Основна властивість відкладання відрізків виражається аксіомою.
Аксіома відкладання відрізків
На будь-якій півпрямій від її початкової точки можна відкласти відрізок заданої довжини, причому тільки один.
6. Відстань між точками
Якщо на прямій відмітити дві різні точки, то вони розіб’ють пряму на три частини, дві з яких - це промені, а та, що знаходиться між променями, називається відрізком.
Відрізок — це частина прямої, що складається з усіх точок цієї прямої, що лежать між двома даними її точками, які називаються кінцями відрізка. Точки відрізка, які лежать між його кінцями, називаються внутрішніми точками відрізка.
Два відрізки називаються рівними, якщо вони мають однакову довжину.
Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його точкою.
Внутрішня точка відрізка, що розбиває його на два рівні відрізки, називається серединою відрізка.
На будь-якому промені від його початку можна відкласти відрізок даної довжини і тільки один.
Відстанню між точками А і В називається довжина відрізка АВ.
Відстань між точками має такі властивості.
- Відстань між різними точками є величиною додатною.
- Відстань від точки А до точки В дорівнює відстані від точки В до точки А, для будь-яких різних точок А і В виконується рівність: АВ=ВА.
- Для будь-яких точок А, В, С відстань між двома точками менша або дорівнює сумі двох інших відстаней:
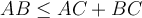 .
.