ЗВИЧАЙНІ ДРОБИ, МІШАНІ ЧИСЛА ТА ДІЇ НАД НИМИ
Звичайні дроби, мішані числа та дії над ними
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | ЗВИЧАЙНІ ДРОБИ, МІШАНІ ЧИСЛА ТА ДІЇ НАД НИМИ |
| Надруковано: | Гість |
| Дата: | Tuesday 24 June 2025 10:13 PM |
Зміст
- 1. Звичайні дроби та мішані числа
- 2. Виділення цілої частини з неправильного дробу. Перетворення мішаного числа в неправильний дріб
- 3. Порівняння дробів та мішаних чисел
- 4. Додавання звичайних дробів та мішаних чисел
- 5. Віднімання звичайних дробів та мішаних чисел
- 6. Множення звичайних дробів
- 7. Ділення дробів
1. Звичайні дроби та мішані числа
Звичайним дробом називається вираз ![]() , де
, де ![]() . Число a називається чисельником, а число b - знаменником. Дробова риска означає знак ділення. Знаменник дробу показує, наскільки рівних частин ділиться число (величина), чисельник – скільки таких частин узято.
. Число a називається чисельником, а число b - знаменником. Дробова риска означає знак ділення. Знаменник дробу показує, наскільки рівних частин ділиться число (величина), чисельник – скільки таких частин узято.
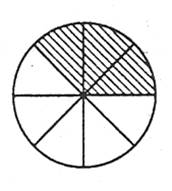
Наприклад, дріб ![]() показує, що якусь величину розділили на 8 рівних частин і взяли три таких частини. 3 - чисельник, 8 - знаменник
показує, що якусь величину розділили на 8 рівних частин і взяли три таких частини. 3 - чисельник, 8 - знаменник ![]() .
.
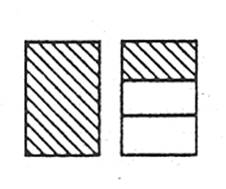
Дріб називається правильним, якщо чисельник менший за знаменник.
Дріб називається неправильним, якщо чисельник дорівнює знаменнику або більший за нього.
Наприклад, дроби ![]() – правильні; дроби
– правильні; дроби ![]() - неправильні.
- неправильні.
Мішаним числом називається сума натурального числа і правильного дробу, записана без знака «+».
Наприклад, число ![]() – мішане, 1 - ціла частина мішаного числа, а
– мішане, 1 - ціла частина мішаного числа, а ![]() – дробова частина мішаного числа.
– дробова частина мішаного числа.
2. Виділення цілої частини з неправильного дробу. Перетворення мішаного числа в неправильний дріб
Щоб із неправильного дробу виділити цілу частину, треба розділити з остачею чисельник на знаменник: неповна частка буде цілою частиною, остача – чисельником, а знаменник – той самий.
Наприклад: ![]() .
.
Щоб подати мішане число у вигляді неправильного дробу, треба помножити його цілу частину на знаменник дробової частини; до одержаного добутку додати чисельник дробової частини і записати суму чисельником, а знаменник залишити той самий.
Наприклад: ![]() .
.
Основна властивість дробу: якщо чисельник і знаменник дробу помножити або поділити на одне і те саме число, відмінне від нуля, то одержимо дріб, який дорівнює даному.
Наприклад: ![]() .
.
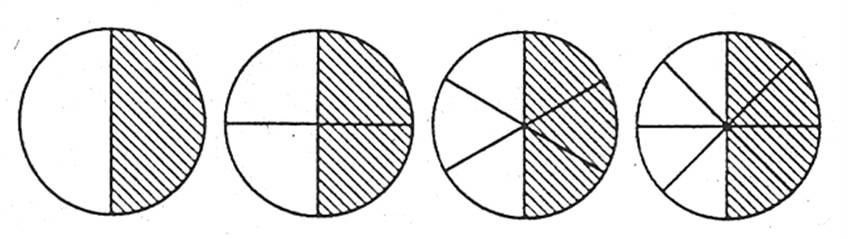
Основна властивість дробу
Скорочення дробу – ділення чисельника і знаменника дробу на спільний дільник чисельника і знаменника дробу, більший за 1.
Наприклад: ![]() .
.
3. Порівняння дробів та мішаних чисел
Із двох дробів із рівними знаменниками більший (менший) той дріб, у якого чисельник більший (менший).
Наприклад: ![]() .
.
Щоб порівняти дроби з різними знаменниками, треба їх звести до спільного знаменника, а потім порівняти.
Наприклад: ![]() ,оскільки
,оскільки ![]() .
.
Із двох мішаних чисел з однаковими цілими частина більше те число, дробова частина якого більша. Із двох мішаних чисел із різними цілими частинами більше те, ціла частина якого більша.
Наприклад: ![]() .
.
4. Додавання звичайних дробів та мішаних чисел
Щоб додати дроби з однаковими знаменниками, треба додати їх чисельники і суму записати в чисельник, а знаменник залишити без змін.
Додавання дробів із рівними знаменниками: ![]() .
.
Наприклад: ![]() .
.
Щоб додати дроби з різними знаменниками, потрібно:
1) звести дроби до найменшого спільного знаменника;
2) додати одержані дроби з однаковими знаменниками.
Додавання дробів із різними знаменниками: ![]() , якщо НСД(b,d)=1.
, якщо НСД(b,d)=1.
Наприклад: ![]() .
.
![]() , де m=НСК(b;d),
, де m=НСК(b;d), ![]() .
.
Наприклад: ![]() .
.
Сумою двох мішаних чисел є мішане число, ціла частина якого є сумою цілих частин доданків, а дробова частина є сумою дробових частин доданків.
Якщо в результаті додавання одержимо мішане число, дробова частина якого є неправильним дробом, треба виділити з неї цілу частину і додати її до цілої частини мішаного числа.
![]()
Наприклад: ![]() .
.
5. Віднімання звичайних дробів та мішаних чисел
Щоб відняти дроби з однаковими знаменниками, треба відняти їх чисельники і різницю записати в чисельник, а знаменник залишити без змін.
Віднімання дробів із рівними знаменниками: ![]() .
.
Наприклад: ![]() .
.
Щоб відняти дроби з різними знаменниками, потрібно:
1) звести дроби до найменшого спільного знаменника;
2) відняти одержані дроби з однаковими знаменниками.
При відніманні звичайних дробів чисельник зменшуваного повинен бути більшим за чисельник від’ємника.
Віднімання дробів із різними знаменниками: ![]() , якщо НСД(b,d)=1.
, якщо НСД(b,d)=1.
Наприклад: ![]() .
.
![]() , де m=НСК(b;d),
, де m=НСК(b;d), ![]() .
.
Наприклад: ![]() .
.
Щоб від одиниці відняти звичайний дріб, треба одиницю подати у вигляді неправильного дробу з однаковими чисельником і знаменником, що дорівнюють знаменнику від’ємника, і виконати віднімання.
Різницею двох мішаних чисел є мішане число, ціла частина якого є різницею цілих частин зменшуваного і від’ємника, а дробова частина є різницею дробових частин зменшуваного і від’ємника.
![]()
Наприклад: ![]() .
.
6. Множення звичайних дробів
Добутком двох звичайних дробів є дріб, чисельник якого дорівнює добутку чисельників цих дробів, а знаменник - добутку їх знаменників.
![]()
Наприклад: ![]() .
.
![]()
Наприклад: ![]() .
.
Щоб знайти дріб від числа, потрібно число помножити на цей дріб.
Два числа, добуток яких дорівнює 1, називають взаємно оберниними.