КУТИ ТА ЇХ ВИДИ. ВЕЛИЧИНА КУТА ТА ЇЇ ВЛАСТИВОСТІ. СУМІЖНІ І ВЕРТИКАЛЬНІ КУТИ
Кути та їх види. Величина кута та її властивості. Суміжні і івертикальні кути
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Геометрія. |
| Книга: | КУТИ ТА ЇХ ВИДИ. ВЕЛИЧИНА КУТА ТА ЇЇ ВЛАСТИВОСТІ. СУМІЖНІ І ВЕРТИКАЛЬНІ КУТИ |
| Надруковано: | Гість |
| Дата: | Wednesday 2 July 2025 4:38 AM |
1. Кут
Кутом називається фігура, яка складається з точки, вершини кута, і двох променів, що виходять із цієї точки (промені називаються сторонами кута). Кут позначається знаком ![]() .
.
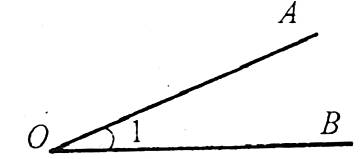
Кут із вершиною О і сторонами ОА і ОВ. Цей кут позначається так: ![]() (літера, яка позначає вершину, завжди ставиться всередині) або
(літера, яка позначає вершину, завжди ставиться всередині) або ![]() . Нерідко кут позначається цифрою:
. Нерідко кут позначається цифрою: ![]() .
.
Кут називається розгорнутим, якщо кожна його сторона є продовженням іншої сторони.
![]()
Два кути називаються рівними, якщо їх можна сумістити накладанням.
Наприклад: ![]() .
.
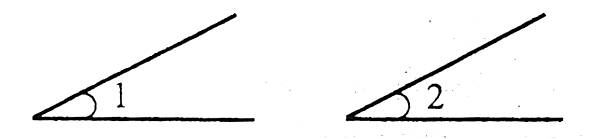
2. Величина кута та її властивості
Основні властивості вимірювання кутів виражаються аксіомами.
Аксіома вимірювання кутів
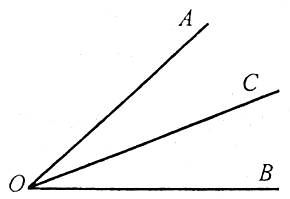
Кожний кут має певну градусну міру, більшу за нуль. Розгорнутий кут дорівнює 180°. Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами, тобто якщо промінь ОС проходить між сторонами кута АОВ, то ![]() .
.
За одиницю вимірювання кутів приймається градус (позначається – 1°) – кут, який дорівнює 1/180 частині розгорнутого кута. Меншими одиницями вимірювання кутів є мінута (позначається знаком ![]() ) і секунда (позначається
) і секунда (позначається ![]() .
.
Додатне число, яке показує скільки разів градус і його частини вкладуються в даному куті, називається градусною мірою кута.
Рівні кути мають рівні градусні міри і навпаки: якщо кути мають рівні градусні міри, то кути рівні.
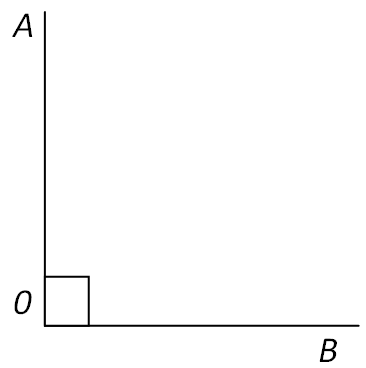
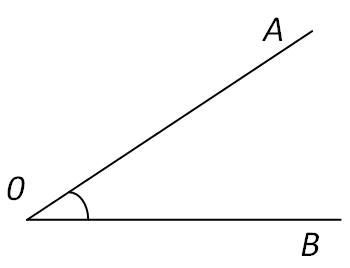
Кут називається прямим, якщо він дорівнює 90° (мал. 1); гострим, якщо він менше 90° (мал. 2); тупим, якщо він більше 90°, але менше 180° (мал. 3).
 |
 |
|
|
Мал.1 |
Мал.2 |
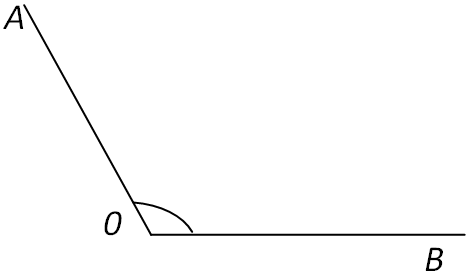
Мал.3
Бісектрисою кута називається промінь, який виходить із вершини кута і поділяє його на два рівних кути.
Наприклад: промінь ОС – бісектриса кута АОВ, оскільки ![]() (рівні кути на мал. позначають однаковими дужками).
(рівні кути на мал. позначають однаковими дужками).
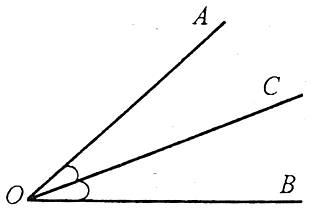
Аксіома відкладання кутів
Від будь-якої півпрямої в задану півплощину можна відкласти кут із даною градусною мірою, меншою 180°, причому тільки один.
3. Суміжні і вертикальні кути та їх властивості
Означення. Суміжними називаються два кути, у яких одна сторона спільна, а дві інші є продовженням одна одної.
Наприклад: кути АОВ і ВОС – суміжні.
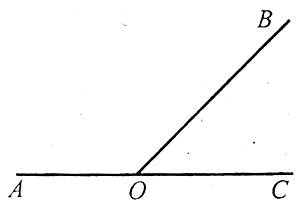
Суміжні кути мають таку властивість.
Теорема. Сума суміжних кутів дорівнює 180°.
Наприклад: ![]() , оскільки
, оскільки ![]() і
і ![]() – суміжні.
– суміжні.
Означення. Вертикальними називаються два кути, у яких сторони одного кута є продовженням сторін другого.
Наприклад: вертикальними кутами будуть ![]() і
і ![]() ;
; ![]() і
і ![]() .
.
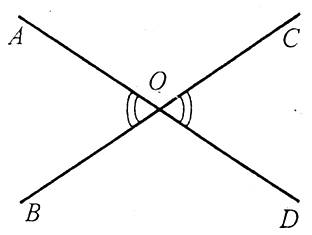
Вертикальні кути мають таку властивість.
Теорема. Вертикальні кути рівні.
![]() , оскільки
, оскільки ![]() і
і ![]() ;
; ![]() і
і ![]() – вертикальні.
– вертикальні.