ДЕСЯТКОВІ ДРОБИ ТА ДІЇ НАД НИМИ
Десяткові дроби та дії над ними
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | ДЕСЯТКОВІ ДРОБИ ТА ДІЇ НАД НИМИ |
| Надруковано: | Гість |
| Дата: | Saturday 27 April 2024 6:31 AM |
1. Десяткові дроби
Звичайні дроби (і мішані числа), знаменниками яких є числа 10, 100, 1000 і т.д., називаються десятковими. Десятковий дріб записують так:
,
де N – ціле число, 
- десяті, соті, тисячні… частини.
Наприклад: 0,25; 3,852; 101,01. – десяткові дроби.
Запис десяткового дробу у вигляді звичайного дробу (мішаного числа) та запис звичайного дробу у вигляді десяткового
Щоб десятковий дріб записати у вигляді звичайного дробу (мішаного числа), треба число, що стоїть до коми, записати цілою частино; число, що стоїть після коми, записати в чисельник, а в знаменнику поставити одиницю і стільки нулів, скільки стоїть цифр після коми.
Наприклад: 
.
Щоб записати дріб у вигляді десяткового, треба чисельник дробу поділити на знаменник.
Наприклад: 
.
2. Порівняння десяткових дробів
Якщо до деякого десяткового дробу дописати праворуч нуль (або кілька нулів), то одержимо дріб, який дорівнює даному.
Якщо деякий десятковий дріб закінчується нулями, то ці нулі можна відкинути й отримати дріб, який дорівнює даному.
Серед двох десяткових дробів менший той дріб, у якого число цілих менше; і більший той, у якого число цілих більше.
Щоб порівняти два десяткові дроби, треба спочатку порівняти цілі частини дробів; у разі їх рівності послідовно порівнюють десяті, якщо рівні десяті – порівнюють соті і т.д.
Наприклад: 10,23>9,85; 3,759<3,81.
3. Наближені значення даного числа
Якщо дане число заміняємо на інше число, близьке за значенням до даного, то одержуємо наближене значення даного числа.
Наприклад: 122≈120 (читаємо: «122 наближено дорівнює 120»), 1,9≈2 (читаємо: «одна ціла дев’ять десятих наближено дорівнює двом»).
Якщо 
,то а називають наближеним значенням числа х із недостачею, а b – наближеним значенням х із надлишком.
4. Округлення десяткових дробів
При округленні десяткових дробів користуються одним із таких двох правил.
Правило 1.
Щоб округлити десятковий дріб до певного розряду дробової частини (до певного десяткового знака), треба:
1) відкинути всі десяткові знаки, які стоять після цього розряду;
2) якщо перша з відкинутих цифр була 5, 6, 7, 8 або 9, то останню залишену цифру збільшити на одиницю;
3) якщо перша з відкинутих цифр була 0, 1, 2, 3 або 4, то останню залишену цифру записати без змін.
Приклад 1. Округлити дріб 3,212 до сотих і дріб 18,091 до десятих.
Розв’язання. 3,212≈3,21; 18,091≈18,1.
Правило 2
Щоб заокруглити десятковий дріб до певного розряду цілої частини вищого розряду одиниць, треба: відкинути всі цифри дробової частини (всі десяткові знаки); цілу частину округлюємо за правилом округлення натуральних чисел.
Приклад 2. Округлити дроби 12 931,3102 і 118,35 до десятків.
Розв’язання. 12 931,3102≈12 930; 118,35≈120.
5. Додавання десяткових дробів
Додавання десяткових дробів виконується порозрядно.
Зручно це виконувати в стовпчик.
При цьому десяткові дроби підписують одне під одним так, щоб кома була під комою. Додають десяткові дроби, як натуральні числа, не зважаючи на коми. У результаті кому ставлять під комами.
Додаючи десяткові дроби з різною кількістю десяткових знаків, пам’ятайте, що цю кількість можна зрівняти, дописавши нулі в кінці числа.
Для десяткових дробів справджуються властивості додавання натуральних чисел.
Наприклад:
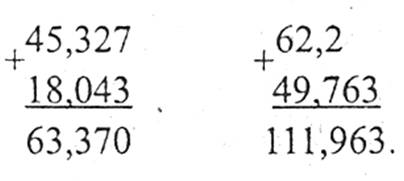
6. Віднімання десяткових дробів
Віднімання десяткових дробів виконується порозрядно.
Зручно це виконувати в стовпчик.
При цьому десяткові дроби підписують одне під одним так, щоб кома була під комою. Віднімають десяткові дроби, як натуральні числа, не зважаючи на коми. У результаті кому ставлять під комами.
Віднімаючи десяткові дроби з різною кількістю десяткових знаків, пам’ятайте, що цю кількість можна зрівняти, дописавши нулі в кінці числа.
Для десяткових дробів справджуються властивості віднімання натуральних чисел.
Наприклад:
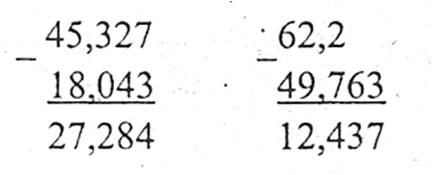
7. Множення десяткових дробів
Щоб помножити два десяткових дроби, треба перемножити їх, не беручи до уваги коми, а потім відділити комою у добутку стільки знаків, скільки їх стоїть справа після коми у двох множниках разом. Якщо в добутку буде менше цифр, ніж потрібно відокремити комою, то попереду дописують потрібну кількість нулів.
Для множення десяткових дробів справджуються всі закони множення.
Щоб помножити десятковий дріб на десять або сто, або тисячу тощо, потрібно в десятковому дробі кому перенести вправо на стільки знаків, скільки нулів стоїть після одиниці у множнику. Якщо десятковий дріб містить меншу кількість десяткових знаків, ніж та, на яку треба перенести кому, то справа від числа приписують необхідну кількість нулів.
Наприклад:
8. Ділення десяткових дробів
Ділення десяткового робу на натуральне число виконується так само, як ділення натуральних чисел, тільки, закінчивши ділення цілої частини числа, треба в частці поставити кому.
Наприклад:
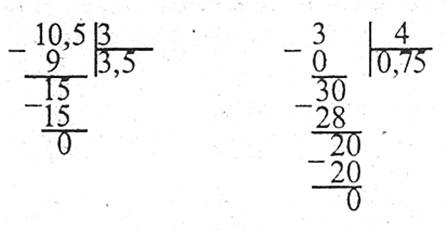
Щоб поділити на десятковий дріб, треба в діленому і дільнику перенести кому вправо на стільки знаків, скільки їх є в дільнику, а потім виконати ділення на натуральне число:
Наприклад:
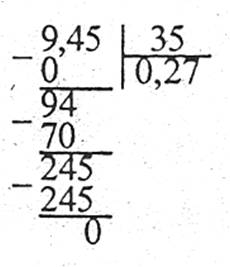
Щоб поділити десятковий дріб на десять або сто, або тисячу тощо, потрібно в десятковому дробі кому перенести вліво на стільки знаків, скільки нулів стоїть після одиниці у дільнику. Якщо ділене містить меншу кількість знаків перед комою, ніж та, на яку треба перенести кому, то зліва від числа приписують необхідну кількість нулів.
Щоб число поділити на десятковий дріб, потрібно у діленому і дільнику кому перенести вправо на стільки знаків, скільки їх стоїть після коми у дільнику, а потім виконати ділення на натуральне число.
Часткою від ділення можуть бути скінченні або нескінченні (періодичні) десяткові дроби.