ПАРАЛЕЛЬНІ ПРЯМІ І ПРЯМІ, ЩО ПЕРЕТИНАЮТЬСЯ
Паралельні прямі і прямі, що перетинаються
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Геометрія. |
| Книга: | ПАРАЛЕЛЬНІ ПРЯМІ І ПРЯМІ, ЩО ПЕРЕТИНАЮТЬСЯ |
| Надруковано: | Гість |
| Дата: | Wednesday 2 July 2025 3:37 PM |
1. Паралельні прямі, прямі, що перетинаються та кути утворені їх перетином
Дві прямі на площині можуть мати спільну точку або не мати спільних точок. Дві прямі, які мають спільну точку, називаються прямими, що перетинаються.
Означення. Дві прямі, які лежать в одній площині і не перетинаються, називаються паралельними.
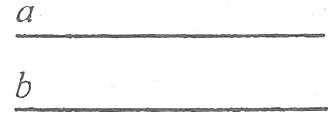
Паралельність прямих позначається знаком ![]() . Паралельність прямих а і b записується так:
. Паралельність прямих а і b записується так: ![]() .
.
Аксіома паралельних прямих
Через точку, яка не лежить на даній прямій, можна провести в площині єдину пряму, паралельну даній прямій.
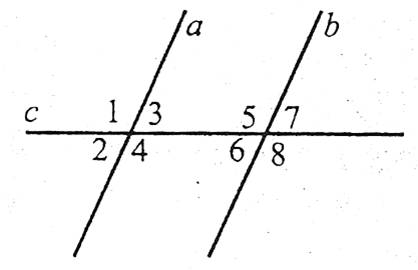
Нехай прямі а і b перетинаються третьою прямою с, яка називається січною. Тоді утворюється вісім кутів, які мають спеціальні назви: кути 3, 4, 5, 6 – внутрішні, кути 1, 2, 7, 8 – зовнішні.
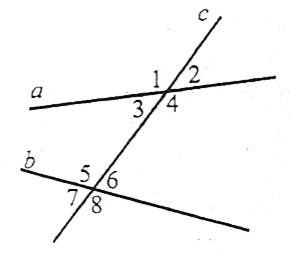
Пари кутів 1 і 5, 2 і 6, 3 і 7, 4 і 8 називаються відповідними, пари кутів 3 і 6, 4 і 5 – внутрішніми різносторонніми, пари кутів 1 і 8, 2 і 7 – зовнішніми різносторонніми. Пари кутів 3 і 5, 4 і 6 називаються, 1 і 7, 2 і 8 – зовнішніми односторонніми.
Якщо дві паралельні прямі а і b перетнуті прямою с, то:
- внутрішні різносторонні кути ріні, тобто
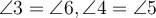 ;
; - сума внутрішніх односторонніх кутів дорівнює 180°, тобто
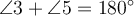 ,
, 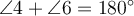 ;
; - відповідні кути рівні, тобто
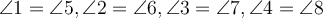 ;
; - зовнішні різносторонні кути рівні, тобто
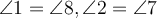 ;
; - сума зовнішніх односторонніх кутів дорівнює 180°, тобто
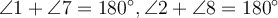 .
.
2. Ознаки паралельності прямих
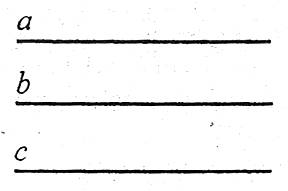
Дві прямі, паралельні третій, паралельні між собою.
Якщо ![]() , то
, то ![]() .
.
Якщо дві прямі а і b перетинаються третьою прямою с, то прямі а і b паралельні, якщо:
- внутрішні різносторонні кути ріні, тобто
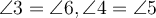 ;
; - сума внутрішніх односторонніх кутів дорівнює 180°, тобто
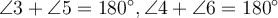 ;
; - відповідні кути рівні, тобто
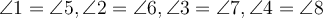 ;
; - зовнішні різносторонні кути рівні, тобто
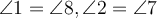 ;
; - сума зовнішніх односторонніх кутів дорівнює 180°, тобто
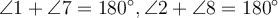 .
.
3. Перпендикулярні прямі
Означення. Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.
Наприклад: перпендикулярні прямі а і b (позначення ![]() , оскільки
, оскільки ![]() .
.
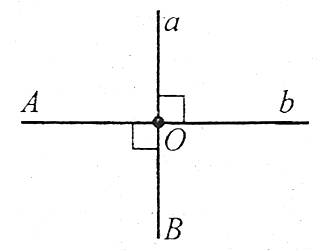
Теорема. Через кожну точку прямої можна провести перпендикулярну їй пряму, причому тільки одну.
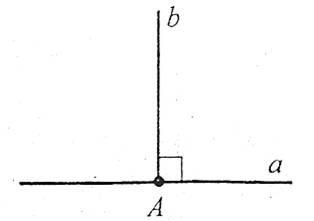
Теорема. Через дану точку поза прямою можна провести перпендикулярну даній пряму, причому тільки одну.
4. Теореми про паралельність і перпендикулярних прямих
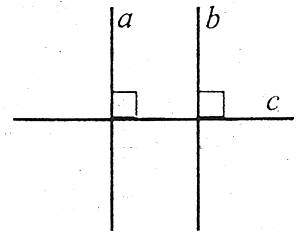
Теорема. Дві прямі перпендикулярні до третьої прямої, паралельні між собою.
Оскільки ![]() , то
, то ![]() .
.
Теорема. Якщо одна із двох паралельних прямих перпендикулярна до третьої, то і друга пряма перпендикулярна до третьої.
Оскільки ![]() , то
, то ![]() .
.
5. Відстань від точки до прямої
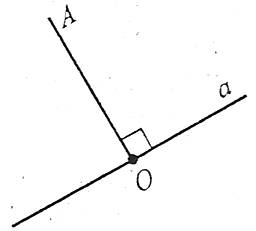
Відстанню від точки до прямої називається довжина перпендикуляра, опущеного із даної точки на дану пряму.
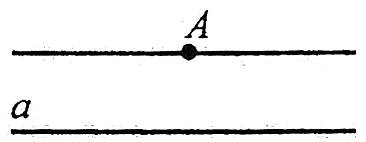
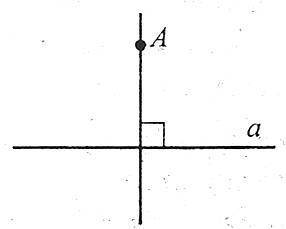
Наприклад: відстанню від точки А до прямої а є довжина перпендикуляра АО.
Відстанню між паралельними прямими називається відстань від будь-якої точки однієї прямої до другої прямої.
Наприклад: відстанню між паралельними прямими а і b є довжина відрізка АО (![]() ).
).
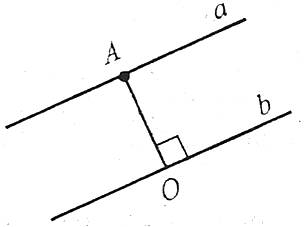
Відстані від усіх точок прямої до паралельної прямої – рівні.