ТРИКУТНИКИ ТА ЇХ ВИДИ. ОЗНАКИ РІВНОСТІ ТРИКУТНИКІВ. РІВНОБЕДРЕНИЙ ТРИКУТНИК ТА ЙОГО ВЛАСТИВОСТІ
Трикутники та їх види. Ознаки рівності трикутників. Рівнобедрений трикутник та його властивості
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Геометрія. |
| Книга: | ТРИКУТНИКИ ТА ЇХ ВИДИ. ОЗНАКИ РІВНОСТІ ТРИКУТНИКІВ. РІВНОБЕДРЕНИЙ ТРИКУТНИК ТА ЙОГО ВЛАСТИВОСТІ |
| Надруковано: | Гість |
| Дата: | Wednesday 4 June 2025 5:44 PM |
1. Трикутник
Трикутник – це геометрична фігура, що складається із трьох точок, які не лежать на одній прямій, і відрізків, які з’єднують ці точки. Точки називають вершинами трикутника, а відрізки – його сторонами.
Наприклад: трикутник із вершинами А, В, С і сторонами АВ, ВС, АС. Цей трикутник позначається так: ![]() .
.
Кути САВ, АВС, АСВ називаються кутами трикутника. Найчастіше їх позначають однією буквою: ![]() . Сторону ВС і кут А трикутника АВС називають протилежними. Протилежними є також сторона АВ і кут С, сторона АС і кут В. Кути А і С, В і С, А і В називаються прилеглими до сторін АС, ВС, АВ.
. Сторону ВС і кут А трикутника АВС називають протилежними. Протилежними є також сторона АВ і кут С, сторона АС і кут В. Кути А і С, В і С, А і В називаються прилеглими до сторін АС, ВС, АВ.
Периметром трикутника називають суму довжин трьох сторін трикутника. Якщо периметр трикутника позначити буквою Р, а довжини сторін ВС, АС і АВ – відповідно, через а, b, с, то
![]() .
.
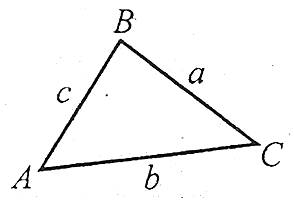
Теорема. У будь-якому трикутнику кожна сторона менша за суму двох інших сторін (нерівність трикутника), тобто ![]() .
.
2. Види трикутників
Залежно від довжини сторін розрізняють різносторонні, рівнобедрені і рівносторонні (або правильні) трикутники.
Трикутник, який має три різні за довжиною сторони, називають різностороннім.
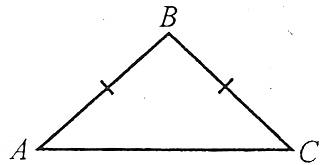
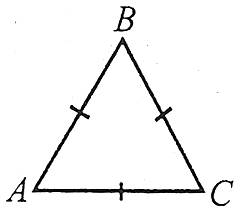
Трикутник, який має дві рівні сторони, називається рівнобедреним. Рівні сторони називаються бічними, а третя сторона – основою трикутника.
Наприклад: ![]() – рівнобедрений, у нього АВ=ВС, тобто АВ, ВС – бічні сторони, АC – основа.
– рівнобедрений, у нього АВ=ВС, тобто АВ, ВС – бічні сторони, АC – основа.
Трикутник, у якого всі сторони рівні, називають рівностороннім, або правильним. У рівностороннього трикутника всі кути рівні, величина кожного з них дорівнює 60°.
Залежно від величини кутів розрізняють гострокутні, прямокутні й тупокутні трикутники.
Гострокутним називається трикутник, у якого всі кути гострі.
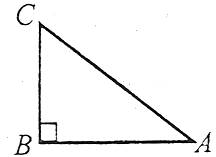
Прямокутним називається трикутник, у якого є прямий кут. Сторону прямокутного трикутника, протилежну прямому куту, називають гіпотенузою, а дві інші сторони – катетами.
Наприклад: сторона АС – гіпотенуза, сторони АВ і ВС – катети.
Тупокутним називається трикутник, у якого є тупий кут.
3. Висоти, бісектриси та медіани трикутника
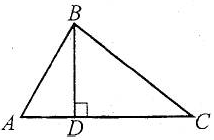
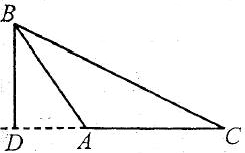
Висотою трикутника називають перпендикуляр, проведений із його вершини до прямої, яка має протилежну сторону.
Наприклад: відрізок BD – висота відповідно гострокутного, тупокутного і прямокутного трикутників.
 |
 |
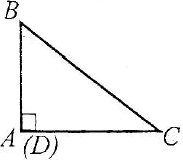 |
Мал.1 |
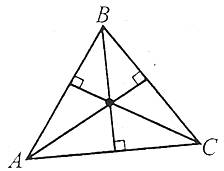
Висоти трикутника або їх продовження перетинаються в одній точці.
Медіаною трикутника називають відрізок, який з’єднує вершину трикутника із серединою протилежної сторони.
Наприклад: ВМ – медіана трикутника АВС.
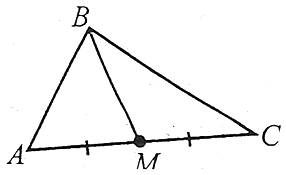
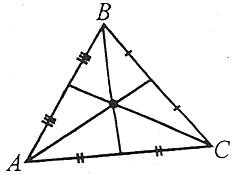
Медіани трикутника перетинаються в одній точці, яка називається центром мас трикутника.
Бісектрисою трикутника називається відрізок, який з’єднує вершину кута і точку протилежної сторони й ділить кут навпіл.
Наприклад: BL – бісектриса трикутника АВС.
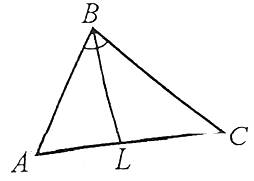
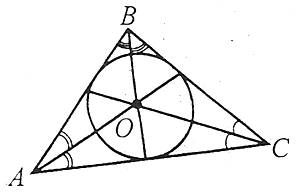
Усі бісектриси трикутника перетинаються в одній точці, яка є центром кола, вписаного в трикутник.
4. Середня лінія трикутника
Середньою лінією трикутника називають відрізок, який з’єднує середини двох його сторін.
Наприклад: MN – середня лінія.
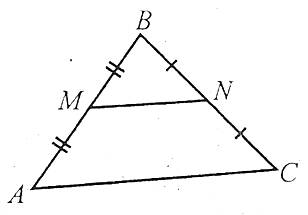
Середня лінія трикутника паралельна третій стороні і дорівнює її половині.
Наприклад: ![]() .
.
5. Поняття про рівність фігур
Перетворення однієї фігури в іншу називається рухом, якщо воно зберігає відстані між точками, тобто будь-які дві точки А і В однієї фігури F переводяться в точки А1 і В1 другої фігури F1 так, що АВ=А1В1.
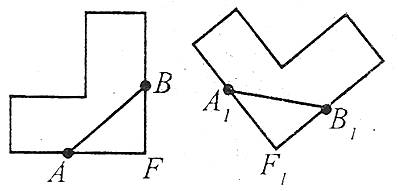
Дві фігури F і F1 називаються рівними, якщо вони рухом перетворюються в одну.
Запис F=F1 означає, що фігура F дорівнює фігурі F1.
Перетворення симетрії відносно точки і відносно прямої та поворот площини навколо точки є рухами.
6. Ознаки рівності трикутників
Наприклад: трикутники АВС і А1В1С1 – рівні.
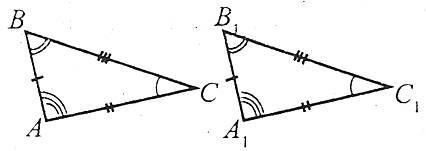
Рівність трикутників позначається так: ![]() .
.
Якщо два трикутники рівні, то елементи (тобто сторони, кути, медіани, бісектриси, висоти тощо) одного з них відповідно дорівнюють елементам другого.
Наприклад: ![]() , АВ=А1В1, ВС=В1С1, АС=А1С1.
, АВ=А1В1, ВС=В1С1, АС=А1С1.
На малюнках рівні відрізки позначаються рівною кількістю рисок, а рівні кути однаковою кількістю дужок. У рівних трикутників проти рівних сторін лежать рівні кути, а проти рівних кутів – рівні сторони.
Перша ознака рівності трикутників (за двома сторонами і кутом між ними)
Якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники є рівними.
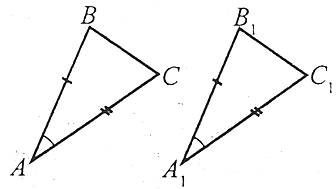
Друга ознака рівності трикутників (за стороною і двома прилеглими кутами)
Якщо сторона і два прилеглі до неї кути одного трикутника відповідно дорівнюють стороні і двом прилеглим до неї кутам другого трикутника, то такі трикутники - рівні.
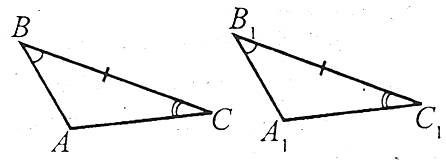
Третя ознака рівності трикутників (за трьома сторонами)
Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам другого трикутника, то такі трикутники є рівними.
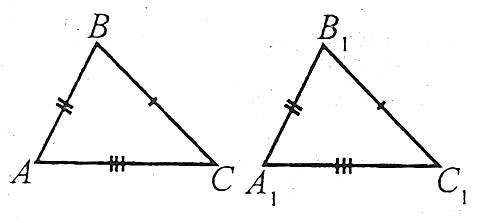
Два прямокутні трикутники рівні, якщо виконується одна з умов:
- два катети одного трикутника відповідно дорівнюють двом катетам другого трикутника;
- катет і гострий кут одного трикутника відповідно дорівнюють катету і гострому куту другого трикутника;
- гіпотенуза і гострий кут одного трикутника дорівнюють гіпотенузі і гострому куту другого трикутника;
- гіпотенуза і катет одного трикутника відповідно дорівнюють гіпотенузі і катету другого трикутника.
7. Властивості та ознаки рівнобедреного трикутника
Властивості рівнобедреного трикутника
Рівнобедрений трикутник має такі властивості.
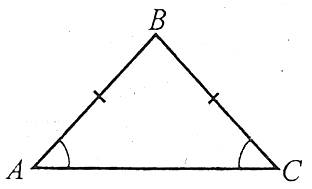
- У рівнобедреного трикутника кути при основі рівні.
Наприклад: АВ=ВС, тобто ![]() – рівнобедрений, отже,
– рівнобедрений, отже, ![]() .
.
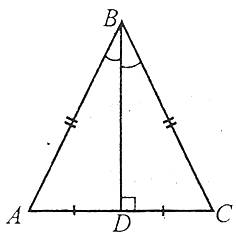
- У рівнобедреного трикутника медіана, проведена до основи, є і бісектрисою, і висотою.
- У рівнобедреного трикутника висота, проведена до основи, є і бісектрисою, і медіаною.
- У рівнобедреного трикутника бісектриса, проведена до основи, є і медіаною, і висотою.
Наприклад: у (АВ=ВС) відрізок BD є і медіаною (AD=DC), і висотою (![]() ), і бісектрисою (
), і бісектрисою (![]() ).
).
Ознаки рівнобедреного трикутника
Якщо в трикутнику:
- два кути рівні,
- медіана і висота збігаються,
- медіана і бісектриса збігаються,
- висота і бісектриса збігаються, то він є рівнобедреним.