ВІДСОТКИ. ЗАДАЧІ НА ВІДСОТКИ
Відсотки. Задачі на відсотки
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | ВІДСОТКИ. ЗАДАЧІ НА ВІДСОТКИ |
| Надруковано: | Гість |
| Дата: | Sunday 1 June 2025 5:56 AM |
1. Відсотки
Соту частину будь-якої величини або числа називають відсотком (процентом). Слово «відсоток» замінюють знаком %, тобто
Наприклад: 1 копійка – один відсоток від гривні, 1 см – один відсоток від метра, тобто
1 коп.=1% грн., 1 см=1% м.
Щоб перетворити десятковий дріб на відсотки, треб його помножити на 100.
Наприклад: 0,35=35%; 0,3=30%; 1,5=150%.
Щоб перетворити відсотки на десятковий дріб, треба число відсотків розділити на 100.
Наприклад: 30%=0,3; 53%=0,53; 1,58%=0,0158.
2. Основні задачі на відсотки
Для того, щоб знайти р відсотків від даного числа а, треба:
1) перевести р відсотків у десятковий дріб;
2) помножити число а на одержаний десятковий дріб.
Приклад 1. Знайти 20% від числа 120.
Розв’язання. 20%=0,2, 120·0,2=24.
Відповідь: 24.
Для того щоб знайти все число за відомою частиною b і числом відповідних відсотків р, треба:
1) перевести р відсотків у десятковий дріб;
2) розділити b на одержаний десятковий дріб.
Приклад 2. Знайти число, 12% якого складає 60.
Розв’язання. 60:0,12=6000:12=500.
Відповідь: 500.
Щоб знайти відсоток числа b від числа а, треба дріб  помножити на 100%.
помножити на 100%.
Приклад 3. Скільки відсотків складає число 0,3 від 20?
Відповідь: 1,5%.
Збільшення (зменшення) числа на декілька відсотків. Формула складних відсотків
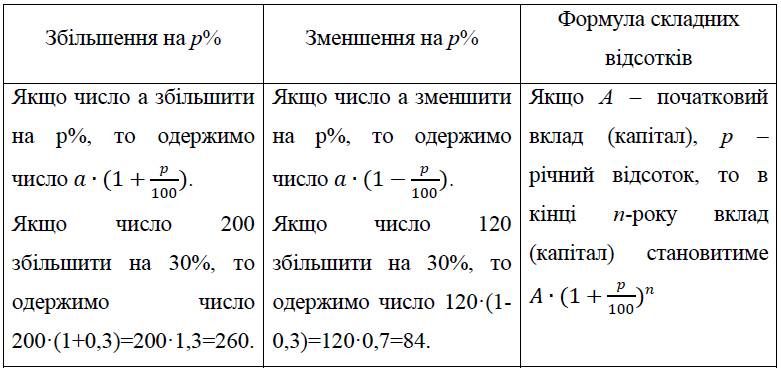
3. Розв'язування більш складних задач на відсотки
Задача 1.
На заводі 40% усіх верстатів переведено на підвищення швидкості, унаслідок чого продуктивність праці зросла на 30%. На скільки відсотків збільшилося виробництво заводської продукції?
Розв’язання
Нехай х – загальний обсяг продукції, що випускав завод раніше.
Знайдемо, на скільки збільшився загальний обсяг продукції: х·0,4·0,3=0,12х.
Знайдемо, на скільки відсотків збільшилося виробництво заводської продукції:
Відповідь: на 12%.
Задача 2.
На скільки відсотків збільшиться продуктивність праці робітників, якщо час на виконання певної операції скоротити на 20%?
Розв’язання
Нехай х – час виконання операції, тоді  - продуктивність праці; 0,8х – час на виконання операції після його скорочення, тоді
- продуктивність праці; 0,8х – час на виконання операції після його скорочення, тоді  - нова продуктивність праці,
- нова продуктивність праці,  - величина, на яку збільшиться продуктивність праці.
- величина, на яку збільшиться продуктивність праці.
Отже, продуктивність праці робітників збільшиться на
Відповідь: на 25%.
Задача 3.
На скільки відсотків збільшиться реальна зарплатня, якщо ціни на всі продовольчі та промислові товари зменшити на 20%?
Розв’язання
Нехай х – початкова ціна товарів, тоді  - реальна заробітна плата. 0,8х – нова ціна товарів, тоді
- реальна заробітна плата. 0,8х – нова ціна товарів, тоді  - реальна заробітна плата. Отже, реальна заробітна плата збільшиться на
- реальна заробітна плата. Отже, реальна заробітна плата збільшиться на
Відповідь: на 25%.




