ПОДІБНІСТЬ ТРИКУТНИКІВ. ТЕОРЕМА ПІФАГОРА
Подібність трикутників. Теорема Піфагора
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Геометрія. |
| Книга: | ПОДІБНІСТЬ ТРИКУТНИКІВ. ТЕОРЕМА ПІФАГОРА |
| Надруковано: | Гість |
| Дата: | Monday 19 May 2025 3:09 AM |
1. Поняття про подібність фігур
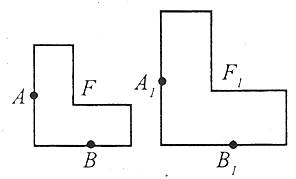
Фігура F1 називається подібною до фігури F (![]() ), якщо існує відображення фігури F на фігуру F1, при якому для будь-яких двох точок А і В фігури F та їх образів А1 і В1 фігури F1 відношення відстаней АВ і А1В1 є величиною сталою.
), якщо існує відображення фігури F на фігуру F1, при якому для будь-яких двох точок А і В фігури F та їх образів А1 і В1 фігури F1 відношення відстаней АВ і А1В1 є величиною сталою.
Число ![]() називають коефіцієнтом подібності.
називають коефіцієнтом подібності.
У подібних фігур відповідні кути рівні, а відповідні відрізки пропорційні.
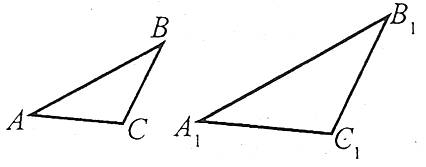
Наприклад: у подібних трикутниках АВС і А1В1С1:
![]() .
.
2. Ознаки подібності трикутників
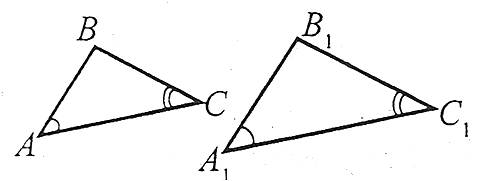
Перша ознака подібності трикутників (за двома кутами)
Якщо два кути одного трикутника відповідно дорівнюють двом кутам другого трикутника, то такі трикутники є подібними.
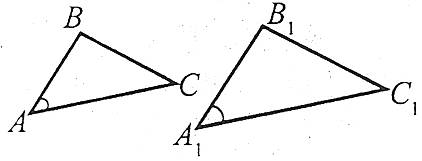
Друга ознака подібності трикутників (за двома сторонами і кутом між ними)
Якщо дві сторони одного трикутника пропорційні двом сторонам другого трикутника і кути, утворені цими сторонами, рівні, то такі трикутники є подібними.
![]()
Третя ознака подібності трикутників (за трьома сторонами)
Якщо три сторони одного трикутника пропорційні трьом сторонам другого трикутника, то такі трикутники є подібними.
![]()
3. Теорема Піфагора та її наслідки
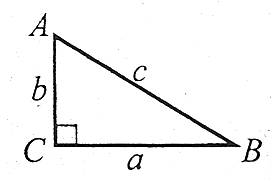
Теорема. У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.
Наприклад: ![]() , або
, або ![]() .
.
Наслідки з теореми Піфагора
- У прямокутному трикутнику будь-який із катетів менший за гіпотенузу.
- Квадрат катета дорівнює різниці квадратів гіпотенузи і другого катета
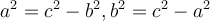 .
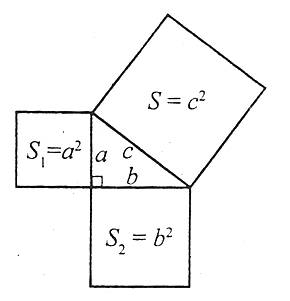
. - Площа квадрата побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі площ квадратів, побудованих на катетах.
Наприклад: ![]() .
.
Теорема, обернена до теореми Піфагора
Якщо квадрат однієї сторони трикутника дорівнює сумі квадратів двох інших сторін, то цей трикутник є прямокутним.