ПОНЯТТЯ ПЛОЩІ. ПЛОЩА ТРИКУТНИКА
Поняття площі. Площа трикутника
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Геометрія. |
| Книга: | ПОНЯТТЯ ПЛОЩІ. ПЛОЩА ТРИКУТНИКА |
| Надруковано: | Гість |
| Дата: | Sunday 29 June 2025 1:40 AM |
1. Поняття площі. Основні властивості площі
Геометричну фігуру називають простою, якщо її можна розбити на скінченне число плоских трикутників (плоским трикутником називається скінченна частина площини, обмежена трикутником).
Площа простої фігури – це додатна величина, числове значення якої має такі властивості:
- рівні фігури мають рівні площі;
- якщо фігура розбивається на частини, кожна з яких є простою фігурою, то площа всієї фігури дорівнює сумі площ її частин;
- площа квадрата зі стороною, яка дорівнює одиниці вимірювання, дорівнює одиниці.
Площа квадрата зі стороною 1 мм, 1 см, 1 дм, 1 м відповідно дорівнює 1 мм2, 1 см2, 1 дм2, 1 м2.
Якщо фігура не є простою, її площу визначають таким чином. Дана фігура має площу S, якщо існують прості фігури, які обмежують її та містяться в ній із площами, що як завгодно мало відрізняються від площі S.
2. Площа трикутника
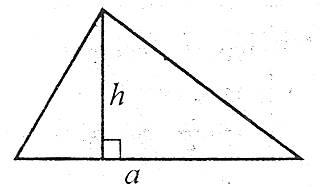
Площа трикутника дорівнює пів добутку його сторони (основи) на проведену до неї висоту:
![]() .
.
Крім того, площу трикутника можна обчислити за формулами.
Наприклад: за формулою Герона:
![]() ,
,
де a, b, c – сторони трикутника, ![]() – його півпериметр.
– його півпериметр.
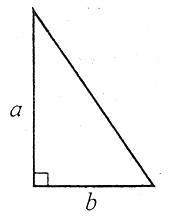
Площа прямокутного трикутника дорівнює половині добутку його катетів:
![]() .
.
Площу правильного (рівностороннього) трикутника можна обчислити за формулою:
![]() ,
,
де а – його сторона.
Площі подібних трикутників відносяться як квадрати відповідних лінійних елементів.