ВПИСАНІ ТА ОПИСАНІ ТРИКУТНИКИ
Вписані та описані трикутники
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Геометрія. |
| Книга: | ВПИСАНІ ТА ОПИСАНІ ТРИКУТНИКИ |
| Надруковано: | Гість |
| Дата: | Friday 4 April 2025 11:59 PM |
1. Властивості серединного перпендикуляра до відрізка
Геометричним місцем точок площини, рівновіддалених від двох даних точок, є серединний перпендикуляр до відрізка, що з’єднує ці дві точки (серединний перпендикуляр – це пряма, що проходить через середину відрізка перпендикулярно до нього).
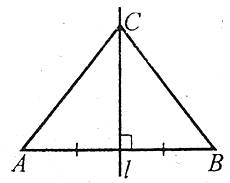
Приклад. Якщо АС=ВС і l – серединний перпендикуляр до відрізка АВ, то С належить l, і навпаки, якщо С належить серединному перпендикуляру l, то СА=СВ.
2. Коло, описане навколо трикутника
Коло називають описаним навколо трикутника, якщо воно проходить через усі його вершини. Трикутник при цьому має назву вписаного.
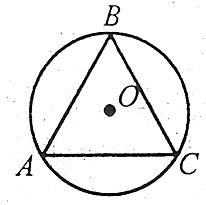
Центр кола, описаного навколо трикутника, є точкою перетину серединних перпендикулярів до сторін трикутника.
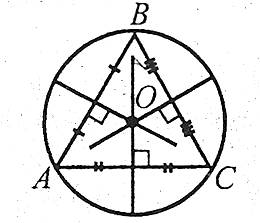
Навколо будь-якого трикутника можна описати коло, причому тільки одне.
Радіус R описаного кола можна обчислити за формулами:
![]() або
або ![]() ,
,
де a, b, c – довжини сторін трикутника, ![]() – півпериметр трикутника, S – його площа.
– півпериметр трикутника, S – його площа.
Радіус R кола, описаного навколо рівностороннього трикутника, можна обчислити за формулою:
![]() ,
,
де а – довжина сторони трикутника.
Радіус R кола, описаного навколо прямокутного трикутника, можна обчислити за формулою:
![]() ,
,
де a, b – довжини катетів прямокутного трикутника, с – довжина його гіпотенузи.
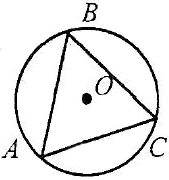
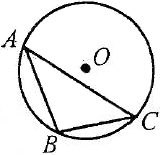
Центр кола, описаного навколо гострокутного трикутника міститься всередині трикутника (мал. 1); описаного навколо тупокутного трикутника – поза трикутником (мал. 2); описаного навколо прямокутного трикутника – на середині гіпотенузи (мал. 3).
 |
 |
|
Мал.1 |
Мал.2 |
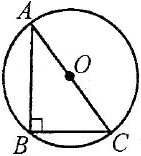
Мал.3
3. Властивості бісектриси кута
Геометричним місцем точок площини, рівновіддалених від сторін даного кута, є його бісектриса.
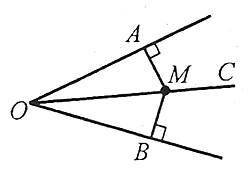
Приклад. Якщо точка М рівновіддалена від сторін кута АОВ (МА=МВ, ![]() ), то точка М лежить на бісектрисі ОС кута АОВ, і навпаки, якщо точка М лежить на бісектрисі кута АОВ, то вона рівновіддалена від його сторін (тобто МА=МВ,
), то точка М лежить на бісектрисі ОС кута АОВ, і навпаки, якщо точка М лежить на бісектрисі кута АОВ, то вона рівновіддалена від його сторін (тобто МА=МВ, ![]() ).
).
4. Коло, вписане в трикутник
Коло називають вписаним в трикутник, якщо воно дотикається до всіх його сторін. Трикутник при цьому називається описаним навколо кола.
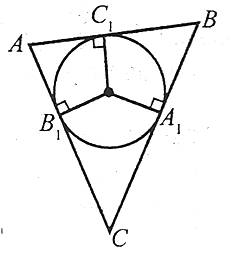
Центр кола, вписаного в трикутник, є точкою перетину його бісектрис.
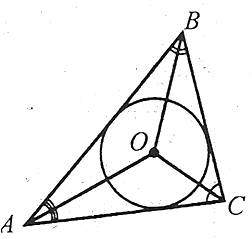
У будь-який трикутник можна вписати коло, причому тільки одне.
Радіус R вписаного кола можна обчислити за формулами:
![]() або
або ![]() ,
,
де a, b, c – довжини сторін трикутника, ![]() – півпериметр трикутника, S – його площа.
– півпериметр трикутника, S – його площа.
Радіус R кола, вписанного в рівносторонній трикутник, можна обчислити за формулою:
![]() ,
,
де а – довжина сторони трикутника, R – радіус кола, описаного навколо трикутника.
Радіус R кола, вписаного в прямокутний трикутник, можна обчислити за формулою:
![]() ,
,
де a, b – довжини катетів прямокутного трикутника, с – довжина його гіпотенузи.