РІВНЯННЯ, НЕРІВНОСТІ ТА ЇХ СИСТЕМИ
Рівняння, нерівності та їх системи
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | РІВНЯННЯ, НЕРІВНОСТІ ТА ЇХ СИСТЕМИ |
| Надруковано: | Гість |
| Дата: | Wednesday 2 July 2025 4:51 AM |
1. Рівняння з однією змінною
Рівнянням називають рівність, яка містить змінну (невідоме).
Розв’язком (коренем) рівняння називається значення змінної, при підстановці якого в рівняння одержують правильну числову рівність.
Наприклад: число 2 – корінь рівняння  , бо
, бо  .
.
Розв’язати рівняння означає знайти його корені або довести, що їх немає.
Два рівняння є рівносильними, якщо множини їх розв’язків збігаються.
Наприклад: рівняння х+2=3 і х-1=0 рівносильні, оскільки вони мають спільний корінь – число 1 й інших коренів не мають.
Розв’язування будь-якого рівняння, як правило, зводиться до заміни його рівносильним рівнянням.
2. Основні теореми про рівносильність рівнянь
1. Якщо до обох частин рівняння додати одне й те саме число або вираз зі змінною, що не втрачає змісту за жодного її значення, то отримаємо рівняння, що є рівносильним даному.
Наприклад: рівняння х+1=3 є рівносильним рівнянню х=2, оскільки друге рівняння можна отримати з першого додаванням до обох частин першого рівняння числа -1 (або перше рівняння можна отримати з другого додаванням до обох частин другого рівняння числа 1).
2. Якщо з однієї частини рівняння перенести в другу частину доданок із протилежним знаком, то отримаємо рівняння, що є рівносильним даному.
Наприклад: рівняння х-3=7 є рівносильним рівнянню х=7+3, тобто рівнянню х=10.
3. Якщо обидві частини рівняння помножити або розділити на одне й те саме число, що не дорівнює нулю, або на вираз зі змінною, який не перетворюється в нуль за жодного значення змінної і не втрачає змісту на множині допустимих значень змінної для даного рівняння, то отримаємо рівняння, що є рівносильним даному.
Наприклад: рівняння 5х=20 є рівносильним рівнянню5х:5=20:5, тобто рівнянню х=4; рівняння  є рівносильним рівнянню
є рівносильним рівнянню  , тобто рівнянню х=-10.
, тобто рівнянню х=-10.
Приклад 1. Розв’яжіть рівняння 5х+3(3х+7)=35.
Розв’язання
Спростимо рівняння: розкриємо дужки в лівій частині рівняння:
5х+9х+21=35.
Перенесемо число 21 із лівої до правої частини рівняння, змінивши знак на протилежний:
5х+9х=35-21.
Зведемо подібні члени в лівій і правій частинах рівняння:
14х=14.
Поділимо ліву і праву частини рівняння на 14. Отже, х=1.
Відповідь: 1.
3. Рівняння із двома змінними
Рівність, яка містить дві змінні (невідомі), називається рівнянням із двома змінними (невідомими).
Наприклад: х-у=4, ху=12 рівняння з двома змінними.
Розв’язком рівняння із двома змінними називають пару значень змінних, які перетворюють це рівняння на правильну числову рівність.
Наприклад: пара чисел х=7 і у=3 є розв’язком 2х-4у=2, оскільки 2·7-4·3=2.
Рівняння із двома змінними, які мають одні і ті самі розв’язки, є рівносильними. Рівняння із двома змінними, які не мають розв’язків, також вважають рівносильними.
У рівнянні із двома змінними можна переносити доданки з однієї частини до другої, змінивши їх знаки. Обидві частини рівняння можна помножити на одне і те саме число або розділити на одне і те саме число, що не дорівнює нулю. При цьому отримаємо рівняння, що є рівносильним даному.
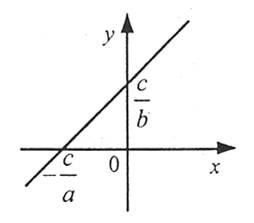
Лінійним рівнянням із двома змінними називають рівняння виду ах+bу=с, де х і у – змінні, а, b, с – числа.
Графіком рівняння із двома змінними називають множину точок координатної площини, координати яких є розв’язками цього рівняння.
Графіком лінійного рівняння із двома змінними, у якому хоча б один із коефіцієнтів при змінних не дорівнює нулю, є пряма.
4. Числові нерівності та їх властивості
Означення. Число а більше числа b, якщо різниця а-b є числом додатним.
Число а менше числа b, якщо різниця а-b є числом від’ємним.
Якщо а більше b, то пишуть: а>b; якщо а менше b, то пишуть: а<b.
Отже, нерівність а>b означає, що різниця а-b є додатною, тобто а-b>0; нерівність а<b означає, що різниця а-b є від’ємною, тобто а-b<0.
Два вирази, які сполучені знаком > або <, називають строгими нерівностями.
Знаки > і < є знаками строгої нерівності, вони протилежні один одному: якщо а>b, то b<а, і навпаки.
Окрім знаків > і <, використовують також знаки:
≥ - більше або дорівнює (не менше),
≤ - менше або дорівнює (не більше).
Невірність а≤b означає, що а<b або а=b, тобто а не більше b.
Наприклад: якщо число учнів вашого класу 30,то число а учнів, які присутні на уроці, може бути меншим або дорівнювати 30. У цьому випадку можна записати: а≤30.
Аналогічно нерівність а≥b означає, що а>b або а=b, тобто а не менше b.
Два вирази, які сполучені знаком ≥ або ≤, називають нестрогими нерівностями. Знаки ≥ і ≤ є знаками нестрогої нерівності.
Наведемо приклади нерівностей:
1) 6<5; 5) 2х+3>2;
2) 7<9; 6) 3х-1>2х+1;
Вираз, який стоїть ліворуч або праворуч від знака нерівності, називають відповідно лівою чи правою частиною нерівності.
Наприклад: лівою частиною нерівності  є вираз
є вираз  , а правою число – 3.
, а правою число – 3.
Якщо обидві частини нерівності – числа, то її називають числовою нерівністю.
Такі нерівності бувають правильні або неправильні.
Наприклад: нерівності 7<9; 4≥4; 4≥1 – правильні, а нерівності 5>6;  - неправильні.
- неправильні.
Теорема 1. Якщо а<b, b<с, то а<с.
Геометрично ця властивість означає: якщо точка А (якій відповідає число а) лежить лівіше від точки В (якій відповідає число b), а точка В, у свою чергу, лежить лівіше від точки С (якій відповідає число с), тоді точка А тим більше буде лежати лівіше від точки С.
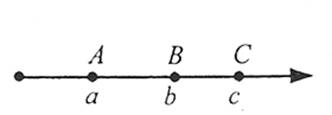
Аналогічно, якщо а>b, b>с, то а>с.
Теорема 2. Якщо а<b і с – будь-яке число, то а+с<b+с.
Отже, якщо до обох частин правильної нерівності додати одне й те саме число, то отримаємо правильну нерівність.
Аналогічно: якщо а>b і с – будь-яке число, то а+с>b+с.
Наслідок. Будь-який доданок можна перенести з однієї частини нерівності в іншу, змінивши знак цього доданка на протилежний.
Теорема 3. Якщо а<b і с>0, то ас<bс. Якщо а<b і с<0, то ас>bс.
Аналогічно: а) якщо а>b і с>0, то ас>bс; б) якщо а>b і с<0, то ас<bс.
Оскільки ділення можна замінити множенням на число, обернене до дільника, то аналогічні властивості є справедливими й для ділення:
Отже, якщо обидві частини правильної нерівності помножити або поділити на одне й те саме додатне число, то отримаємо правильну нерівність.
Якщо обидві частини правильної нерівності помножити або поділити на одне й те саме від’ємне число і замінити знак нерівності на протилежний, то отримаємо правильну нерівність.
Теорема 4. Якщо а>b і с>d, то а+с>b+d.
Якщо почленно додати правильні нерівності одного знака, то одержимо правильну нерівність.
Наприклад:
Теорема 5. Якщо а<b, с<d і а>0, b>0, с>0, d>0, то ас<bd.
Якщо почленно перемножити правильні нерівності одного знака, ліві і праві частини яких є додатними числами, то отримаємо правильну нерівність.
Наприклад:
Слід зазначити, що теореми 4 і 5 справедливі для трьох і більше нерівностей.
5. Нерівність з однією змінною
Нерівністю зі змінною (невідомим) називають два вирази зі змінною (невідомим), між якими стоїть один зі знаків нерівності: > (більше), < (менше), ≥ (більше або дорівнює; не менше); ≤ (менше або дорівнює; не більше).
Наприклад:  - нерівності з однією змінною.
- нерівності з однією змінною.
Розв’язком нерівності з однією змінною називають значення змінної, яке перетворює нерівність на правильну числову нерівність.
Наприклад: число 2 – розв’язок нерівності х+3>4, а число -1 не є розв’язком даної нерівності.
Приклад 2. Доведіть, що при кожному дійсному значенні а нерівність  є справедливою.
є справедливою.
Доведення
Складемо різницю лівої і правої частин нерівностей й перетворимо її:
При будь-якому значенні а утворена різниця  – додатна, тому що значення виразу
– додатна, тому що значення виразу  є невід’ємним, а значення виразу
є невід’ємним, а значення виразу  – додатним. Отже, при будь-якому значенні а нерівність
– додатним. Отже, при будь-якому значенні а нерівність  є справедливою.
є справедливою.
Розв’язати нерівність з однією змінною означає знайти всі її розв’язки або довести, що розв’язків немає.
Розв’язками нерівності є деяка множина чисел.
У таблиці наведено деякі числові множини, їх позначення, зображення на координатній прямій і запис у вигляді нерівності.
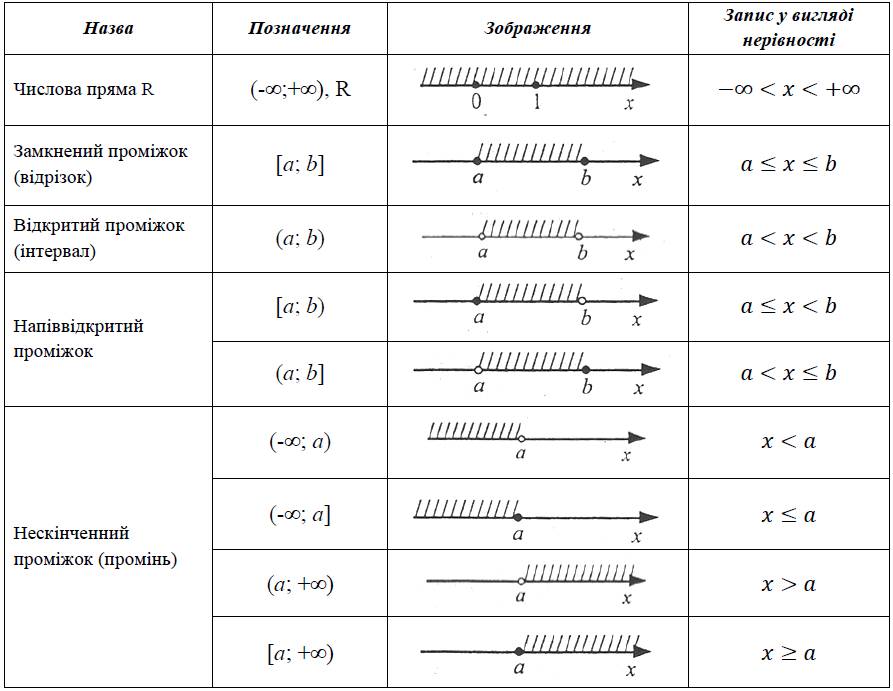
Розв’язування нерівностей, як правило, зводиться до заміни даної нерівності нерівністю, яка їй рівносильна.
Нерівності, які мають одні й ті самі розв’язки, називаються рівносильними. Нерівності, які не мають розв’язків, також вважаються рівносильними.
Нерівності з однією змінною мають такі властивості:
1. Якщо з однієї частини нерівності перенести в другу доданок із протилежним знаком, то одержимо рівносильну їй нерівність.
Наприклад: нерівність х+2>3 рівносильна нерівності х+2-2>3-2, тобто х>1.
2. Якщо обидві частини нерівності помножити або поділити на одне й те саме додатне число, то отримаємо рівносильну їй нерівність.
Наприклад:  рівносильна нерівності
рівносильна нерівності  , тобто х>6.
, тобто х>6.
3. Якщо обидві частини нерівності помножити або поділити на одне й те саме від’ємне число, змінивши знак нерівності на протилежний, то одержимо рівносильну їй нерівність.
Наприклад: нерівність -2х<10 рівносильна нерівності -2х:(-2)>10:(-2), тобто х>-5.
Приклад 3. Розв’яжіть нерівність 2(х-5)+6≥9х-2(х-3).
Розв’язання
Перетворимо ліву і праву частини нерівності, тобто розкриємо дужки:
2х-10+6≥9х-2х+6.
Перенесемо члени, що містять змінну до лівої частини нерівності, а члени, які не містять змінну, у праву частину нерівності, при цьому змінимо знаки членів на протилежні:
2х-9х+2х≥10-6+6.
Зведемо подібні в лівій і правій частинах нерівності:
-5х≥10.
Поділимо обидві частини нерівності на -5, змінивши знак нерівності на протилежний:
х≤-2.
Отже, розв’язком нерівності є проміжок (-∞;-2].
Відповідь: (-∞;-2].
6. Системи рівнянь із двома змінними
Декілька рівнянь із двома змінними, відносно яких поставлено завдання знайти всі спільні розв’язки, називають системою рівнянь із двома змінними. Систему рівнянь позначають зліва фігурною дужкою, що їх об’єднує.
Наприклад:
 - системи рівнянь із двома змінними.
- системи рівнянь із двома змінними.
Розв’язати систему рівнянь із двома змінними означає знайти всі її розв’язки або довести, що система розв’язків не має.
Розв’язком системи рівнянь із двома змінними називають пару значень змінних, яка перетворює кожне рівняння системи на правильну рівність.
Наприклад: пара чисел х=3, у=2 (записують так(3;2)) є розв’язком системи рівнянь
Розв’язування системи рівнянь із двома змінними, як правило, зводиться до заміни даної системи рівносильною їй системою.
Системи рівнянь із двома змінними, які мають одні й ті самі розв’язки, називають рівносильними. Системи рівнянь, які не мають розв’язків, також вважають рівносильними.
Системи рівнянь мають такі властивості:
1. Якщо замінити порядок рівнянь заданої системи, то одержимо систему рівносильну даній.
Наприклад: системи
2. Якщо одне з рівнянь системи замінити на рівносильне йому рівняння, то одержимо систему, рівносильну даній.
Наприклад: системи
3. Якщо в системі рівнянь з одного рівняння виразити одну змінну, наприклад у, через іншу змінну, і одержаний вираз підставити замість у в друге рівняння системи, то одержимо систему, рівносильну даній.
Наприклад: системи
4. Якщо перше рівняння системи замінити сумою першого рівняння, помноженого на число α≠0, і другого рівняння, помноженого на число β≠0, а друге рівняння залишити без змін, то одержимо систему, рівносильну даній.
Наприклад:
7. Системи нерівностей з однією змінною
Декілька нерівностей з однією змінною, відносно яких поставлено завдання знайти всі спільні розв’язки, називають системою нерівностей з однією змінною. Системою нерівностей позначають зліва фігурною дужкою, що їх об’єднує.
Наприклад:
 - системи нерівностей з однією змінною.
- системи нерівностей з однією змінною.
Розв’язком системи нерівностей з однією змінною називають значення змінної, при якому кожна нерівність перетворюється на правильну числову.
Наприклад: х=3 є розв’язком системи нерівностей
Розв’язати систему нерівностей означає знайти всі її розв’язки або довести, що розв’язків немає.
Розв’язування системи нерівностей з однією змінною, як правило, зводиться до заміни даної системи рівносильною їй системою.
Щоб розв’язати систему нерівностей з однією змінною слід:
1) розв’язати кожну нерівність;
2) знайти спільні розв’язки даних нерівностей.
Приклад 4. Розв’яжіть систему нерівностей
Розв’язання
Маємо
Зобразимо на координатній прямій множини розв’язків кожної з нерівностей.
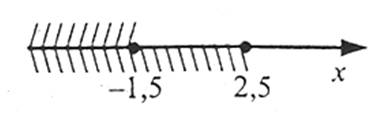
Обидві нерівності справедливі при х≤-1,5. Відповідь можна записати у вигляді нерівності х≤-1,5 або числового проміжку (-∞;-1,5].
Відповідь: (-∞;-1,5].













