ФУНКЦІЇ ТА ЇХ ОСНОВНІ ВЛАСТИВОСТІ
Функції та їх основні властивості
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | ФУНКЦІЇ ТА ЇХ ОСНОВНІ ВЛАСТИВОСТІ |
| Надруковано: | Гість |
| Дата: | Tuesday 1 July 2025 8:25 AM |
Зміст
- 1. Поняття функції. Основні способи задання функції. Область визначення і область значень функції
- 2. Графік функції
- 3. Зростання і спадання функції
- 4. Періодичність функції
- 5. Парні та непарні функції
- 6. Графіки деяких функцій та їх основні властивості
- 7. Перетворення графіків функцій
- 8. Функція, обернена до даної
1. Поняття функції. Основні способи задання функції. Область визначення і область значень функції
Числовою функцією з областю визначення D називають залежність, згідно з якою кожному числу х із множини D відповідає за деяким правилом єдине число у із множини Е.
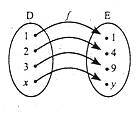
Змінну х називають незалежною змінною або аргументом функції, а змінну у – залежною змінною або функцією.
Функцію позначають латинськими буквами f, g, h,… (або f(x), g(x), h(x),…) або рівностями y=f(x), y=g(x), y=h(x),…
Якщо задане конкретне значення незалежної змінної  , то
, то  називається значенням функції f у точці
називається значенням функції f у точці  .
.
Область визначення функції позначають D(f). Множина, що складається з усіх чисел f(x) таких, що х належить області визначення функції f, називається областю значень функції і позначається Е(f).
Розглянемо приклад. Результати вимірювання температури тіла хворого залежно від часу подано в таблиці:
|
Час доби, х (год) |
9 |
12 |
15 |
18 |
21 |
24 |
|
Температура тіла, y=f(x) (C°) |
39 |
38,5 |
38,3 |
37,3 |
37,1 |
37 |
Залежність y=f(x) є функцією, де х – незалежна змінна, у – залежна змінна.
f(9)=39; f(12)=38,5; f(15)=38,3; f(18)=37,3; f(21)=37,1; f(24)=37.
D(f)={9; 12; 15; 18; 21; 24}.
Е(f)={39;38,5; 38,3; 37,3; 37,1; 37}.
Функцію можна задати за допомогою таблиці, графіка, формули.
Найчастіше функцію задають формулою, яка дає можливість одержати значення залежної змінної у, підставивши конкретне значення аргументу х.
Наприклад: якщо кожному значенню х із множини дійсних чисел відповідає квадрат цього числа, то функцію можна записати у вигляді формули:  , або
, або  .
.
Областю визначення функції у=f(х), яка задана формулою, називають множину тих значень, яких може набувати х, тобто таких х, за яких формула має зміст (усі дії, указані формулою, можна виконати).
При знаходженні області визначення слід пам’ятати:
1. Якщо функція є многочленом  , то
, то  .
.
2. Якщо функція має вигляд  , де
, де  – многочлени, то слід вважати g(x)≠0 (знаменник дробу не дорівнює 0).
– многочлени, то слід вважати g(x)≠0 (знаменник дробу не дорівнює 0).
Наприклад: якщо  , то
, то  . Тоді х≠1 і х≠-1. Отже,
. Тоді х≠1 і х≠-1. Отже,  .
.
3. Якщо функція має вигляд  , то слід вважати f(x)≥0 (арифметичний квадратний корінь існує тільки з невід’ємних чисел).
, то слід вважати f(x)≥0 (арифметичний квадратний корінь існує тільки з невід’ємних чисел).
2. Графік функції
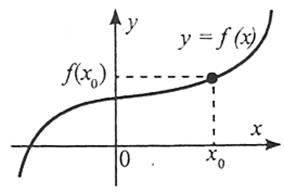
Графіком функції  називають множину всіх точок площини з координатами
називають множину всіх точок площини з координатами  , де перша координата «пробігає» всю область визначення функції
, де перша координата «пробігає» всю область визначення функції  , а друга – це відповідні значення функції у точці х.
, а друга – це відповідні значення функції у точці х.
3. Зростання і спадання функції
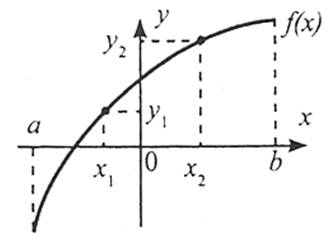
Функція  є зростаючою, якщо більшому значенню аргументу відповідає більше значення функції. Тобто для будь-яких значень
є зростаючою, якщо більшому значенню аргументу відповідає більше значення функції. Тобто для будь-яких значень  з області визначення функції як таких,
з області визначення функції як таких,  , що виконується нерівність
, що виконується нерівність  (або
(або  ), і навпаки, якщо
), і навпаки, якщо  - зростаюча, то за умови
- зростаюча, то за умови  виконується нерівність
виконується нерівність  .
.
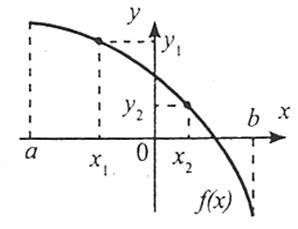
Функція  є спадною, якщо більшому значенню аргументу відповідає менше значення функції. Тобто для будь-яких значень
є спадною, якщо більшому значенню аргументу відповідає менше значення функції. Тобто для будь-яких значень  з області визначення функції як таких,
з області визначення функції як таких,  , що виконується нерівність
, що виконується нерівність  (або
(або  ), і навпаки, якщо
), і навпаки, якщо  - спадна, то за умови
- спадна, то за умови  виконується нерівність
виконується нерівність  .
.
4. Періодичність функції
Функцію  називають періодичною з періодом Т≠0, якщо для будь-якого х з області визначення числа х+Т і х-Т також належать області визначення і виконується рівність:
називають періодичною з періодом Т≠0, якщо для будь-якого х з області визначення числа х+Т і х-Т також належать області визначення і виконується рівність:
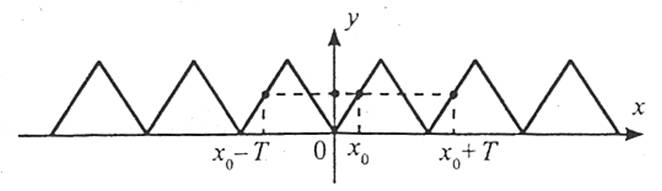
Якщо функція  - періодична з найменшим додатним періодом Т, то функція
- періодична з найменшим додатним періодом Т, то функція  теж періодична, і найменший додатний період її дорівнює
теж періодична, і найменший додатний період її дорівнює  .
.
5. Парні та непарні функції
Функція  є парною, якщо для будь-якого значення х із D(y) значення – х також належить D(y) і виконується рівність
є парною, якщо для будь-якого значення х із D(y) значення – х також належить D(y) і виконується рівність  . Графік парної функції симетричний відносно осі ОY.
. Графік парної функції симетричний відносно осі ОY.
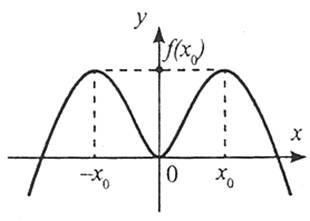
Приклад 1. Чи є парною функція  ?
?
Оскільки  і
і  , то функція парна.
, то функція парна.
Приклад 2. Чи є парною функція  ?
?
Оскільки  , але
, але  , то функція є непарною.
, то функція є непарною.
Функція  є непарною, якщо для будь-якого значення х із D(y) значення
є непарною, якщо для будь-якого значення х із D(y) значення  і виконується рівність
і виконується рівність  . Графік непарної функції симетричний відносно початку координат.
. Графік непарної функції симетричний відносно початку координат.
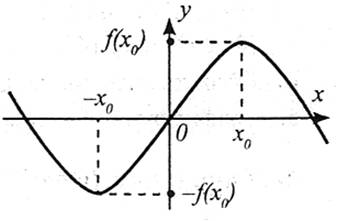
Приклад 3. Чи є непарною функція  ?
?
Оскільки  і
і  , то функція є непарною.
, то функція є непарною.
6. Графіки деяких функцій та їх основні властивості
Властивості:
1. Область визначення: R.
2. Функція є непарною.
3. Для  функція зростає, якщо
функція зростає, якщо  ; спадає, якщо
; спадає, якщо  .
.
4. Область значень: R.
5. Графік – пряма, що проходить через початок координат.
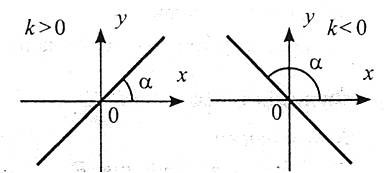
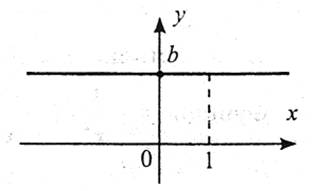
Властивості:
1. Область визначення: R.
2. Функція є парною. Якщо b=0, то функція і парна, і непарна.
4. Область значень: {b}.
5. Графік – пряма, паралельна осі х, якщо b≠0, і пряма, що збігається з віссю х, якщо b=0.
6. Функція періодична, будь-яке число є періодом. Найменшого додатного періоду немає.
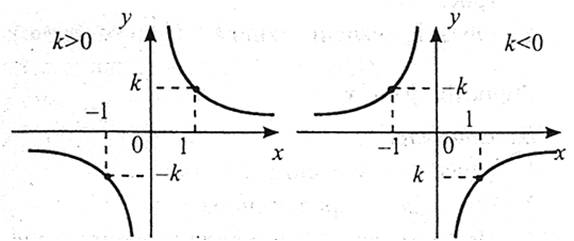
Властивості
2. Функція є непарною.
3. Якщо  , функція спадає на проміжку
, функція спадає на проміжку  і на проміжку
і на проміжку  . Якщо
. Якщо  , функція зростає на проміжку
, функція зростає на проміжку  і на проміжку
і на проміжку  .
.
5. Графік функції – гіпербола.
Властивості
1. Область визначення: R.
2. Функція є парною.
3. Якщо  , функція спадає на проміжку (-∞;0], зростає на проміжку [0;+∞). Якщо
, функція спадає на проміжку (-∞;0], зростає на проміжку [0;+∞). Якщо  , функція зростає на проміжку (-∞;0], спадає на проміжку [0;+∞).
, функція зростає на проміжку (-∞;0], спадає на проміжку [0;+∞).
4. Область значень: якщо  , то
, то  ; якщо
; якщо  , то
, то ![y \in ( - \infty ;0] y \in ( - \infty ;0]](http://zno.academia.in.ua/filter/tex/pix.php/da2ff11ec731c92def4b7cdc46a61fc1.gif) .
.
5. Графік функції – парабола.
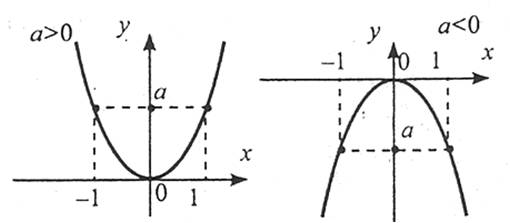
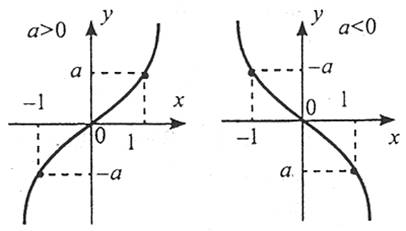
Властивості
1. Область визначення: R.
2. Функція є непарною.
3. Для  функція зростає, якщо
функція зростає, якщо  ; спадає, якщо
; спадає, якщо  .
.
4. Область значень: R.
5. Графік функції – кубічна парабола.
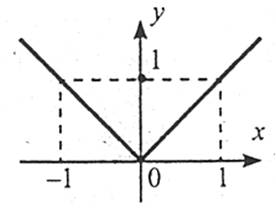
Властивості
1. Область визначення: R.
2. Функція є парною.
3. На проміжку (-∞;0] функція спадає; на проміжку [0;+∞) функція зростає.
4. Область значень: [0;+∞).
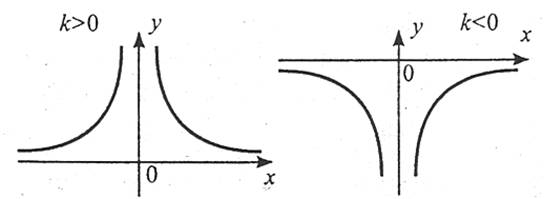
Властивості
2. Функція є парною.
3. Якщо  , функція зростає на проміжку
, функція зростає на проміжку  і спадає на проміжку
і спадає на проміжку  . Якщо
. Якщо  , функція спадає на проміжку
, функція спадає на проміжку  і зростає на проміжку
і зростає на проміжку  .
.
4. Область значень: якщо  , то
, то  ; якщо
; якщо  , то
, то  .
.
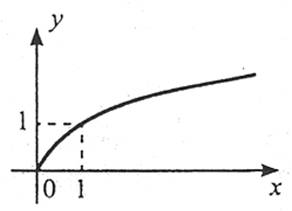
Властивості
1. Область визначення: [0;+∞).
2. Функція ні парна, ні непарна.
3. На проміжку [0;+∞) функція зростає.
4. Область значень: [0;+∞).
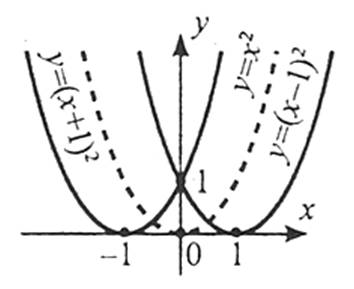
7. Перетворення графіків функцій
1. Щоб побудувати графік функції  , слід перенести графік функції f(x) уздовж осі Ох на а одиниць: вправо, якщо а<0; вліво, якщо а>0.
, слід перенести графік функції f(x) уздовж осі Ох на а одиниць: вправо, якщо а<0; вліво, якщо а>0.
2. Щоб побудувати графік функції  , слід перенести графік функції f(x) уздовж осі Оy на b одиниць: вверх, якщо b<0; вниз, якщо b>0.
, слід перенести графік функції f(x) уздовж осі Оy на b одиниць: вверх, якщо b<0; вниз, якщо b>0.
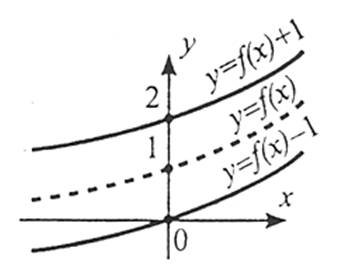
3. Щоб побудувати графік функції  , слід графік функції
, слід графік функції  симетрично відобразити відносно осі абсцис.
симетрично відобразити відносно осі абсцис.
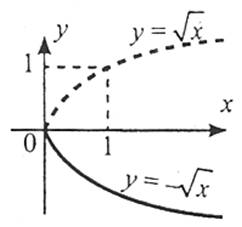
4. Щоб побудувати графік функції  , слід графік функції
, слід графік функції  симетрично відобразити відносно осі ординат.
симетрично відобразити відносно осі ординат.
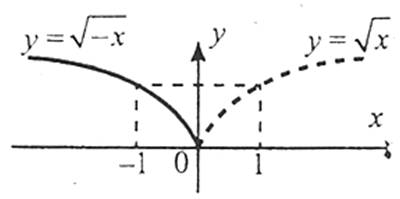
5. Щоб побудувати графік функції  , слід частину графіка функції
, слід частину графіка функції  у верхній півплощині і на осі абсцис залишити без змін, а замість частини графіка в нижній півплощині побудувати симетричну їй частину відносно осі Ох.
у верхній півплощині і на осі абсцис залишити без змін, а замість частини графіка в нижній півплощині побудувати симетричну їй частину відносно осі Ох.
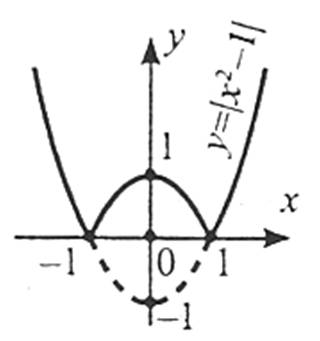
6. Щоб побудувати графік функції  , слід частину графіка функції
, слід частину графіка функції  у правій півплощині і на осі ординат залишити без змін, а замість частини графіка в лівій півплощині побудувати симетричну їй частину відносно осі Оу.
у правій півплощині і на осі ординат залишити без змін, а замість частини графіка в лівій півплощині побудувати симетричну їй частину відносно осі Оу.
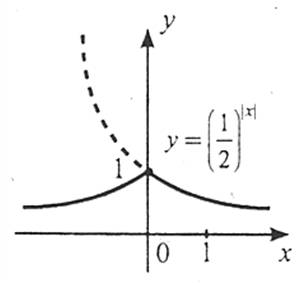
7. Щоб побудувати графік функції  , слід:
, слід:
1) при k>1 стиснути графік функції  до точки (0;0) уздовж осі абсцис у k разів;
до точки (0;0) уздовж осі абсцис у k разів;
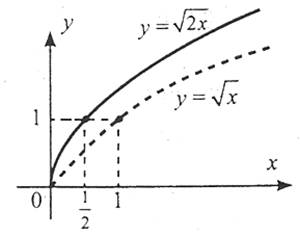
2) при 0<k<1 розтягнути від точки (0;0) графік функції  уздовж осі абсцис у
уздовж осі абсцис у  разів.
разів.
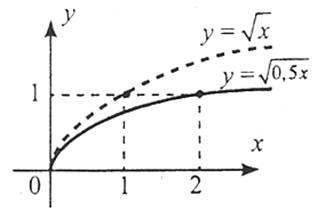
8. Щоб побудувати графік функції  , слід:
, слід:
1) при k>1 розтягнути графік функції  до точки (0;0) уздовж осі ординат у k разів;
до точки (0;0) уздовж осі ординат у k разів;
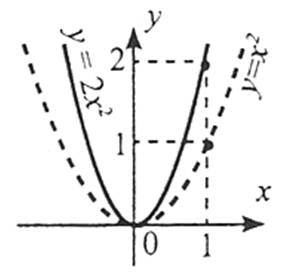
2) при 0<k<1 стиснути від точки (0;0) графік функції  уздовж осі ординат у
уздовж осі ординат у  разів.
разів.
8. Функція, обернена до даної
Функцію, яка набуває кожного свого значення в єдиній точці області визначення, називають оборотною.
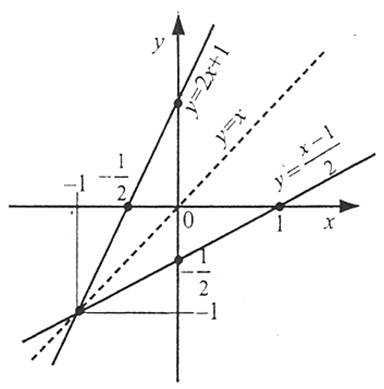
Наприклад: функція у=2х+1 – оборотна, а функція  (визначена на всій числовій осі) не є оборотною.
(визначена на всій числовій осі) не є оборотною.
Якщо функція задана формулою  , то для знаходження оберненої функції потрібно розв’язати рівняння
, то для знаходження оберненої функції потрібно розв’язати рівняння  відносно х, а потім поміняти місцями х і у.
відносно х, а потім поміняти місцями х і у.
Наприклад: оберненою до функції  є функція
є функція  .
.
Якщо рівняння  відносно х має більше ніж один корінь, то функція
відносно х має більше ніж один корінь, то функція  не має оберненої функції.
не має оберненої функції.
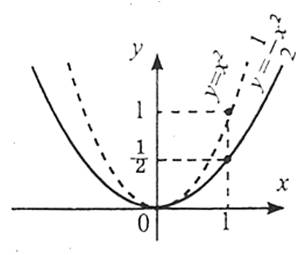
Наприклад: функція  оберненої функції не має.
оберненої функції не має.
Графіки даної функції і оберненої до неї симетричні відносно прямої у=х.
Наприклад: функції  , графіки яких симетричні відносно прямої у=х, є оберненими.
, графіки яких симетричні відносно прямої у=х, є оберненими.
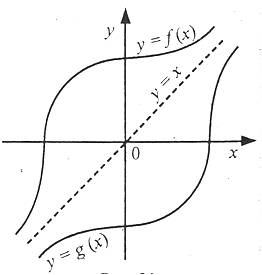
Якщо функція  зростає (спадає) на деякому проміжку, то вона оборотна. Функція, яка обернена до даної і визначена в області значень функції
зростає (спадає) на деякому проміжку, то вона оборотна. Функція, яка обернена до даної і визначена в області значень функції  , також є зростаючою (спадною).
, також є зростаючою (спадною).
Якщо функція  визначена на області визначення D і має область значень Е, то обернена функція має область визначення Е і область значень D.
визначена на області визначення D і має область значень Е, то обернена функція має область визначення Е і область значень D.





















