РОЗВ'ЯЗУВАННЯ ДОВІЛЬНИХ ТРИКУТНИКІВ
Розв'язування довільних трикутників
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Геометрія. |
| Книга: | РОЗВ'ЯЗУВАННЯ ДОВІЛЬНИХ ТРИКУТНИКІВ |
| Надруковано: | Гість |
| Дата: | Thursday 3 July 2025 9:05 AM |
1. Теореми синусів і косинусів
Теорема косинусів. Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними.
Наприклад: у ![]() ,
, ![]() .
.
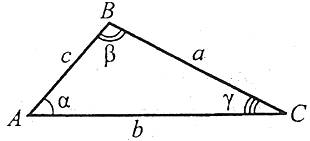
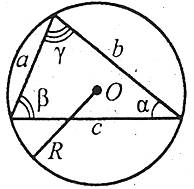
Теорема синусів. У довільному трикутнику відношення будь-якої сторони до синуса протилежного кута стале і дорівнює діаметру описаного навколо нього кола:
![]() .
.
Варто пам’ятати, що синуси суміжних кутів рівні, а їх косинуси – протилежні числа:
![]() .
.
2. Розв'язування трикутників
Розв’язуванням трикутників називається знаходження всіх його шести елементів (тобто трьох сторін і трьох кутів) за будь-якими трьома елементами, що визначають трикутник.
Розглянемо три задачі на розв’язування трикутників. При цьому будемо використовувати такі позначення для сторін трикутника АВС: АВ=с, ВС=а, СА=b.
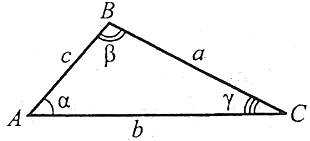
Задача 1. Дано: а, b, ![]() . Знайти: с,
. Знайти: с, ![]() ,
, ![]() (розв’язування трикутника за двома сторонами і кутом між ними).
(розв’язування трикутника за двома сторонами і кутом між ними).
Розв’язування
За теоремою синусів знаходимо с:
![]() .
.
Користуючись теоремою косинусів, маємо:
![]() .
.
Далі ![]() .
.
Задача 2. Дано: а, ![]() ,
, ![]() . Знайти:
. Знайти: ![]() , b, с (розв’язування трикутника за стороною і двома прилеглими кутами).
, b, с (розв’язування трикутника за стороною і двома прилеглими кутами).
Розв’язання
![]() .
.
За теоремою синусів знаходимо b і с:
![]() .
.
Задача 3. Дано а, b, с. Знайти: ![]() ,
, ![]() ,
, ![]() (розв’язування трикутника за трьома сторонами).
(розв’язування трикутника за трьома сторонами).
Розв’язання
Користуючись теоремою косинусів, знаходимо: ![]() , звідси
, звідси ![]() .
.
Аналогічно знаходимо ![]() . Тоді
. Тоді ![]() .
.