МНОГОКУТНИКИ ТА ЇХ ВЛАСТИВОСТІ
Многокутники та їх властивості
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Геометрія. |
| Книга: | МНОГОКУТНИКИ ТА ЇХ ВЛАСТИВОСТІ |
| Надруковано: | Гість |
| Дата: | Saturday 26 April 2025 8:28 AM |
1. Основні теоретичні відомості
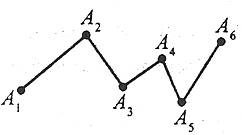
Ламаною А1А2А3…Аn називають фігуру, що складається з точок А1,А2,А3,…Аn, які називають вершинами ламаної, і відрізків А1А2, А2А3, …Аn-1Аn, які називають ланками ламаної. А1 і Аn називають кінцями ламаної.
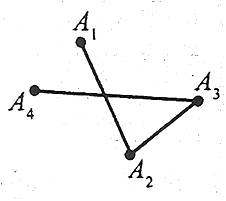
Ламана називається простою, якщо вона не має точок само перетину.
Наприклад: ламана з точкою самоперетину.
Ламану називають замкненою, якщо її кінці збігаються.
Довжиною ламаної називається сума довжин її ланок.
Довжина ламаної не менша від довжини відрізка, що з’єднує її кінці.
2. Многокутники та їх види
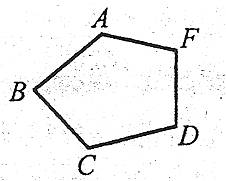
Многокутником називається проста замкнена ламана, сусідні ланки якої не лежать на одній прямій. Вершини ламаної називають вершинами многокутника, а ланки ламаної – сторонами многокутника. Дві вершини многокутника, які належать до однієї сторони називають сусідніми. Відрізки, що з’єднують несусідні вершини многокутника, називають діагоналями многокутника.
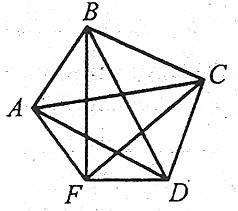
Наприклад: АС, АD, BF, BD, CF – діагоналі многокутника ABCDF.
Многокутник із n вершинами (із n сторонами) називають n-кутником.
Наприклад: п’ятикутник.
Плоским многокутником називають скінченну частину площини, обмежену многокутником.
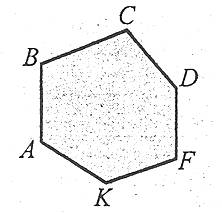
Многокутник називають опуклим, якщо він лежить по один бік від кожної прямої, яка містить його сторону.
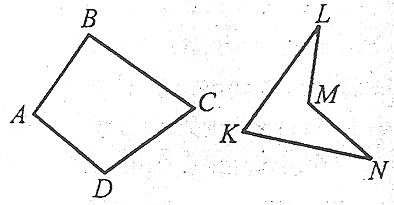
Наприклад: чотирикутник ABCD – опуклий, а чотирикутник KLMN – не опуклий.
3. Сума кутів опуклого многокутника
Кутом многокутника при даній вершині називають кут, утворений його сторонами, які сходяться в цій вершині.
Сума кутів опуклого многокутника дорівнює ![]() .
.
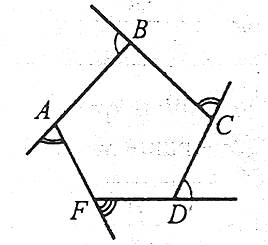
Зовнішнім кутом многокутника при даній вершині називають кут, суміжний із внутрішнім кутом многокутника при цій вершині.
Сума зовнішніх кутів опуклого n-кутника, взятих по одному при кожній вершині, дорівнює 360°.
Наприклад: ![]() .
.