Многогранники. Призми, їх види та властивості
Многогранники. Призми, їх види та властивості
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Геометрія. |
| Книга: | Многогранники. Призми, їх види та властивості |
| Надруковано: | Гість |
| Дата: | Saturday 21 June 2025 6:52 AM |
1. Многогранники
У стереометрії, крім точок, прямих та площин, розглядають просторові геометричні фігури, не всі точки яких лежать в одній площині. Прикладом просторової фігури може служити геометричне тіло – частина простору, яку займає предмет. Куб, прямокутний паралелепіпед, тетраедр – приклади геометричних тіл.
Куб – це тіло, поверхня якого обмежена шістьма рівними квадратами.
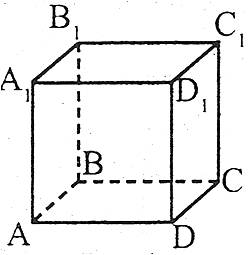
Прямокутний паралелепіпед – це тіло, поверхня якого обмежена шістьма прямокутниками.
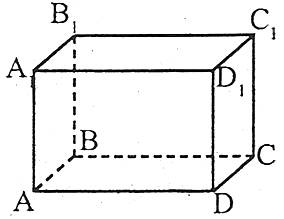
Тетраедр – це тіло, поверхня якого обмежена чотирма трикутниками.
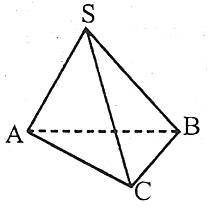
Правильним тетраедром називається тіло, поверхня якого обмежена чотирма рівними правильними трикутниками.
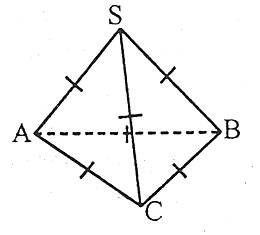
Многогранником називається тіло, поверхня якого обмежена числом плоских многокутників. Многокутники, що обмежують поверхню тіла, називають гранями, сторони граней – ребрами, вершини граней – вершинами многогранника.
2. Призми
Призма (n-кутна) – це многогранник, у якого дві грані рівні n-кутники, які лежать у паралельних площинах, а інші n граней – паралелограми.
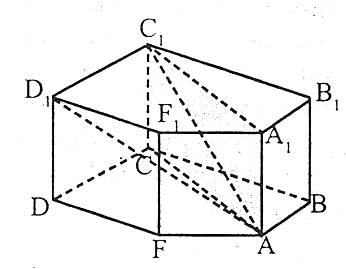
Многокутники називаються основами призми, а паралелограми – бічними гранями. Сторони бічних граней та основ називаються ребрами призми. Кінці ребер називаються вершинами призми. Бічними ребрами називаються ребра, які не належать основам.
Властивості призми
- Основи призми паралельні і рівні.
- Бічні ребра паралельні і рівні.
- Бічні грані – паралелограми.
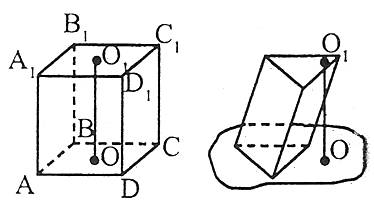
Висотою призми називається перпендикуляр, проведений із точки верхньої основи на площину нижньої основи.
Наприклад: ОО1 – висота призми.
Діагоналлю призми називається відрізок, який з’єднує дві вершини, які не належать одній грані.
Наприклад: АС1, АD1 – діагоналі призми.
Діагональним перерізом призми називається переріз її площиною, яка проходить через два бічних ребра, що не належать одній грані.
Наприклад: АА1СС1 – діагональний переріз призми.
Прямою призмою називається призма, у якої бічні ребра перпендикулярні до площини основ. Призма, яка не є прямою, називається похилою.
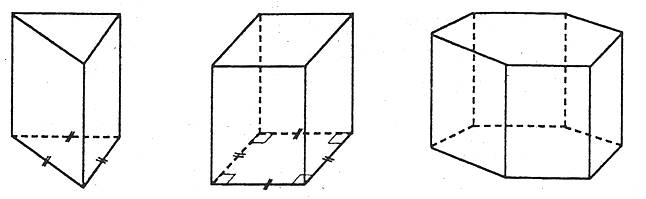
Правильною призмою називається пряма призма, в основі якої лежить правильний многокутник.
Наприклад: правильні трикутна, чотирикутна та шестикутна призми.
3. Паралелепіпед
Паралелепіпедом називається призма, основи якої є паралелограмами.
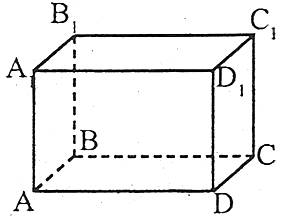
Властивості паралелепіпеда
- Протилежні грані паралелепіпеда попарно рівні та паралельні.
- Усі діагоналі паралелепіпеда перетинаються в одній точці та діляться нею навпіл.
Паралелепіпед називається прямим, якщо в нього бічні ребра перпендикулярні до основ. Прямий паралелепіпед має всі властивості паралелепіпеда, і, крім того, бічні грані прямого паралелепіпеда є прямокутниками.
Прямий паралелепіпед, основами якого є прямокутники, називається прямокутним.
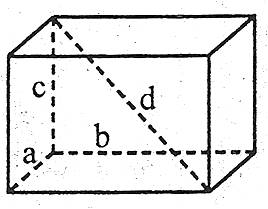
Усі грані прямокутного паралелепіпеда – прямокутники. Довжини трьох ребер прямокутного паралелепіпеда, які виходять з однієї вершини, називаються лінійними розмірами (або вимірами) прямокутного паралелепіпеда.
Властивості прямокутного паралелепіпеда
- Усі діагоналі рівні.
- Квадрат діагоналі дорівнює сумі квадратів трьох його вимірів.
Наприклад: ![]() .
.
Прямокутний паралелепіпед, у якого всі ребра рівні, називається кубом.