Піраміди, їх види та властивості
Піраміди, їх види та властивості
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Геометрія. |
| Книга: | Піраміди, їх види та властивості |
| Надруковано: | Гість |
| Дата: | Saturday 21 June 2025 7:14 AM |
1. Піраміди
Пірамідою (n-кутною) називається многогранник, у якого одна грань є довільним n-кутником, а інші n граней – трикутники, які мають спільну вершину. N-кутник називається основою, а трикутники – бічними гранями. Спільна вершина бічних граней називається вершиною піраміди.
Наприклад: піраміда SABCD, ABCD – основа; ![]() – бічні грані піраміди; S – вершина піраміди; SA, SB, SC, SD – бічні ребра.
– бічні грані піраміди; S – вершина піраміди; SA, SB, SC, SD – бічні ребра.

Висотою піраміди називається перпендикуляр, проведений із вершини піраміди на площину основи.
Наприклад: SO – висота піраміди.
Правильною називається піраміда, в основі якої лежить правильний многокутник, а висота піраміди співпадає з центром цього многокутника.
Висота бічної грані правильної піраміди, проведеної із вершини піраміди, називається її апофемою.
Наприклад: правильна трикутна піраміда SABC, ![]() , SK – апофема.
, SK – апофема.
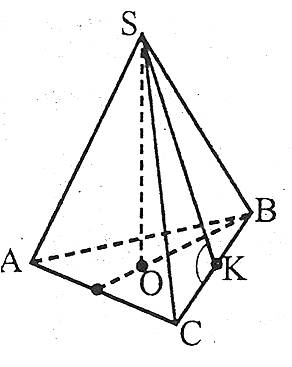
У правильній піраміді:
- бічні ребра рівні;
- бічні грані рівні;
- апофеми рівні;
- двогранні кути при основі рівні;
- двогранні кути при бічних ребрах рівні;
- кожна точка висоти правильної піраміди рівновіддалена від усіх вершин основи;
- кожна точка висоти правильної піраміди рівновіддалена від усіх бічних граней;
- кожна точка висоти правильної піраміди рівновіддалена від усіх бічних ребер.
Діагональним перерізом піраміди називається переріз площиною, яка проходить через два бічних ребра піраміди, що не належать одній грані.
2. Властивості паралельних перерізів пірамід
Теорема. Якщо піраміда перерізається площиною, паралельною основі, то:
- бічні ребра та висота піраміди діляться цією площиною на пропорційні частини;
- переріз – многокутник, подібний основі;
- площі перерізу та основи відносяться як квадрати їх відстаней від вершини піраміди.
Якщо довільну n-кутну піраміду перерізати площиною, паралельною основі, то ця площина відітне від піраміди многогранник, дві грані якого подібні n-кутники, а інші n граней – трапеції. Цей многогранник називається зрізаною пірамідою.
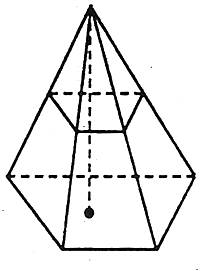
Паралельні грані зрізаної піраміди називаються основами, а всі інші – бічними. Висотою зрізаної піраміди називається перпендикуляр, проведений з будь-якої точки однієї основи на площину іншої основи.
Зрізана піраміда називається правильною, якщо вона складає частину правильної піраміди. Висота бічної грані правильної зрізаної піраміди, проведена до ребра основи, називається апофемою.
У правильній зрізаній піраміді:
- бічні ребра рівні;
- бічні грані рівні;
- апофеми рівні;
- двогранні кути при кожній основі рівні;
- двогранні кути при бічних ребрах рівні;
- кожна точка прямої, яка проходить через центри її основ, рівновіддалена від усіх вершин кожної основи, рівновіддалена від площини бічних граней, рівновіддалена від прямих, на яких лежать бічні ребра.