Площі поверхонь та об'єм многогранників
Площі поверхонь та об'єм многогранників
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Геометрія. |
| Книга: | Площі поверхонь та об'єм многогранників |
| Надруковано: | Гість |
| Дата: | Thursday 2 January 2025 4:33 PM |
1. Формули площі поверхонь і об'ємів призми
Площею бічної поверхні призми є сума площ її бічних граней.
Площею повної поверхні призми є сума площ усіх її граней.
Площа бічної поверхні прямої призми дорівнює добутку периметра основи на висоту призми, тобто на довжину бічного ребра.
Наприклад: 
.
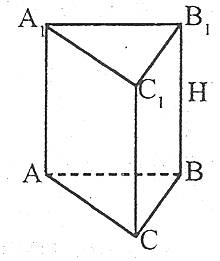
Площу бічної поверхні призми можна обчислити за формулою:
,
де Р – периметр перпендикулярного перерізу (перерізу призми площиною, яка перпендикулярна до бічних ребер і перетинає всі її бічні ребра), АА1 – довжина бічного ребра.
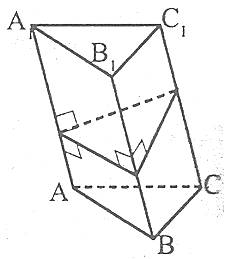
Площа повної поверхні призми (
) дорівнює сумі площі бічної поверхні (
) і площ двох основ (
):
.
Об'єм V призми дорівнює добутку площі основи на висоту:
.
Об'єм V призми можна обчислити за формулою
,
де 
— площа перпендикулярного перерізу, АА1—довжина бічного ребра.
Об'єм прямокутного паралелепіпеда дорівнює добутку його вимірів:
.
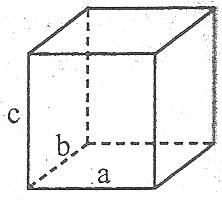
Об'єм V куба дорівнює кубу його ребра:
.
2. Формули площі поверхонь і об'ємів піраміди
Площею повної поверхні піраміди є сума площ усіх її граней (тобто основи і бічних граней), а площею бічної поверхні піраміди — сума площ її бічних граней:
.
Наприклад: 
.
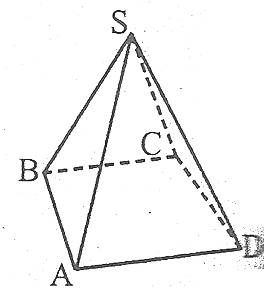
Площа бічної поверхні правильної піраміди дорівнює половині добутку периметра основи на апофему:
де l – апофема.
Наприклад: 
.
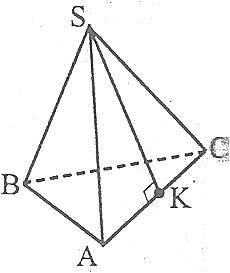
Якщо бічні грані піраміди нахилені до основи під кутом φ, а площа основи дорівнює 
, то площа бічної поверхні піраміди
.
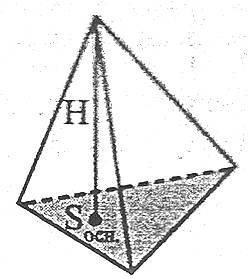
Об’єм піраміди дорівнює третині добутку площі основи на висоту:
.
Площа повної поверхні зрізаної піраміди дорівнює сумі площ усіх її граней (тобто основ і бічних граней), а площа бічної поверхні зрізаної піраміди – сумі площ її бічних граней
.
Наприклад: 
, де 
.
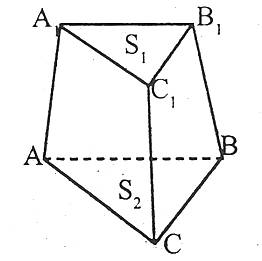
Площа бічної поверхні правильної зрізаної піраміди дорівнює добутку півсуми периметрів основ на апофему.
,
де Р1, Р2 – периметри основ, l – апофема.
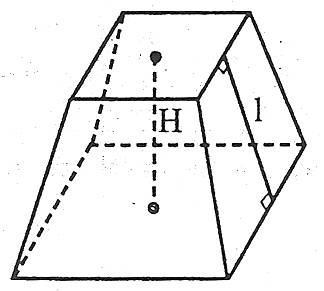
Об’єм V зрізаної піраміди, висота якої H, а площі основ дорівнюють S1 і S2, обчислюється за формулою:
.