Площі поверхонь та об'єми тіл обертання
Площі поверхонь та об'єми тіл обертання
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Геометрія. |
| Книга: | Площі поверхонь та об'єми тіл обертання |
| Надруковано: | Гість |
| Дата: | Saturday 26 April 2025 8:33 AM |
1. Формули площі поверхні та об'єму циліндра
Якщо поверхню циліндра розрізати по колах основ і якійсь твірній, а потім розгорнути її на площині, то утвориться розгортка циліндра.
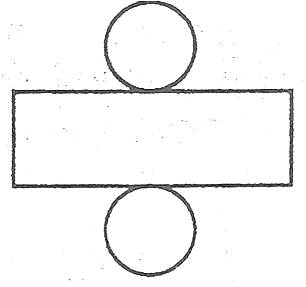
Площею поверхні циліндра називається площа його розгортки.
Площа поверхні циліндра ![]() дорівнює сумі площ основ
дорівнює сумі площ основ ![]() і бічної поверхні
і бічної поверхні ![]() :
:
![]() .
.
Оскільки
![]() ,
,
де R – радіус основи циліндра, Н – його висота, то
![]() .
.
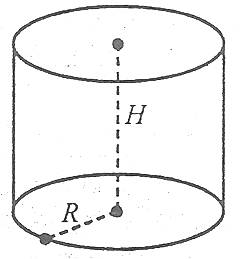
Об’єм циліндра дорівнює добутку площі основи на висоту, тобто
![]() .
.
2. Формули площі поверхні та об'єму конуса
Площа бічної поверхні конуса дорівнює півдобутку довжини кола основи на його твірну, тобто
![]() .
.
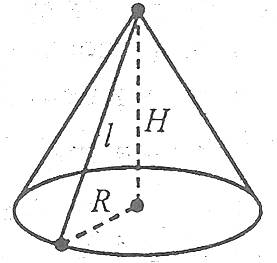
Площа повної поверхні конуса дорівнює сумі площ бічної поверхні і площі основи:
![]() .
.
Об’єм конуса дорівнює третині добутку площі основи на висоту конуса, тобто
![]() .
.
Площа бічної поверхні зрізаного конуса дорівнює півдобутку суми довжин кіл основ на довжину твірної, тобто
![]() ,
,
де l – твірна, R і r – радіуси основ.
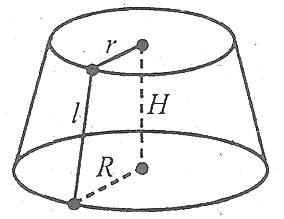
Площа повної поверхні зрізаного конуса дорівнює сумі площі бічної поверхні і площ основ:
![]() .
.
Об’єм зрізаного конуса обчислюється за формулою:
![]() ,
,
де R і r – радіуси основ, Н – висота конуса.
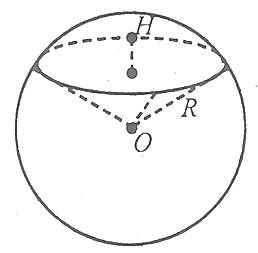
3. Формули площі поверхні сфери, об’єму кулі
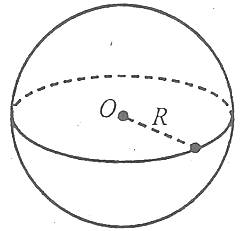
Площа поверхні сфери знаходиться за формулою
![]() ,
,
де R – радіус сфери.
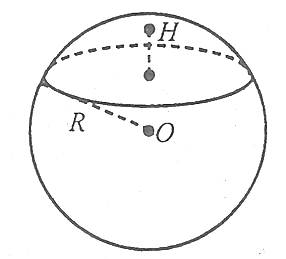
Площа сферичного сегмента обчислюється за формулою
![]() ,
,
де R – радіус сфери, а Н – висота сегмента.
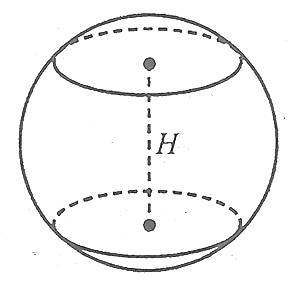
Площа сферичного поясу (кільця) знаходиться за формулою
![]() ,
,
де R – радіус сфери, а Н – висота поясу (кільця).
Об’єм кулі обчислюється за формулою
![]() ,
,
де R – радіус кулі.
Об’єм кульового сегмента обчислюється за формулою
![]() ,
,
де R – радіус кулі, Н – висота кульового сегмента.
Об’єм кульового сектора обчислюється за формулою
![]() ,
,
де R – радіус кулі, Н – висота відповідного кульового сегмента.