Декартові координати у просторі
Декартові координати у просторі
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Геометрія. |
| Книга: | Декартові координати у просторі |
| Надруковано: | Гість |
| Дата: | Friday 10 January 2025 11:14 AM |
1. Визначення декартових координат у просторі
Декартова система координат у просторі задається трійкою попарно перпендикулярних осей (вісь ОХ – вісь абсцис, вісь ОУ – вісь ординат, вісь OZ – вісь аплікат), які мають спільний початок О (початок координат) і однаковий масштаб уздовж осей.
Кожній точці простори за певним правилом ставиться у відповідність трійка чисел – абсциса, ордината та апліката (х;у;z). які називаються декартовими координатами точки. Ці координати визначаються в такий спосіб: через точку А проводимо три площини, паралельні координатним площинам YOZ, XOZ, XOY. Із координатними осями OX, OY, OZ площини перетнуться в точках хА, уА, zA. Число х, абсолютна величина якого дорівнює довжині відрізка ОХА, називається абсцисою точки А. Це число буде додатним, якщо хА належить додатній півосі ОХ, і від’ємним, якщо лежить на від’ємній півосі.
Аналогічно визначаються ордината у та апліката z точки А.
Декартові координати у просторі записують у дужках поруч із буквеним позначенням точки А(х;у;z), причому першою в дужках стоїть абсциса, другою – ордината, третьою – апліката.
Для точок площини ХОY апліката z дорівнює нулю, для точок площини XOZ – ордината у дорівнює нулю, для точок площини YOZ – абсциса х дорівнює нулю.
Наприклад: точка А має координати 2;3;3, що записується так: А(2;3;3).
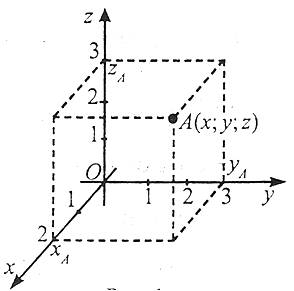
Будь-якій трійці чисел х, у, z відповідає лише одна точка площини А(х;у;z).
Приклад 1. Задано точки А(1;2;3), В(0;1;2), С(1;0;0), D(1;0;2). Які з цих точок лежать: 1) у площині XOZ; 2) на осі ОХ; 3) у площині YOZ?
Розв’язання
- Якщо точка лежить у площині XOZ, то координата у дорівнює 0, у площині XOZ лежать точки С(1;0;0), D(1;0;2).
- Якщо точка лежить на осі ОХ, то координата у і z дорівнюють нулю, отже, на осі ОХ лежить точка С(1;0;0).
- У площині YOZ лежить точка В(0;1;2).
Відповідь: 1) С, D; 2) С; 3) В.
2. Відстань між двома точками
Відстань між двома точками дорівнює квадратному кореню із суми квадратів різниць однойменних координат.
Відстань між двома точками в просторі
![]() ,
,
де d – відстань між точкою А1 із координатами (х1;у1;z1) і точкою А2 із координатами (х2;у2;z2).
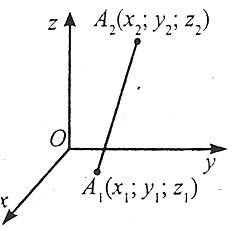
Приклад 2. Задано точки А(1;2;3), В(2;3;1), С(3;1;2). Знайдіть периметр трикутника АВС.
Розв’язання
Оскільки
![]() ,
,
![]() ,
,
![]() ,
,
то ![]() .
.
Відповідь: ![]() .
.
3. Координати середини відрізка
Координати середини відрізка дорівнюють півсумі відповідних координат його кінців.
Координати середини відрізка на площині
Координати (хс;ус;zc) точки С, що є серединою відрізка, визначаються за формулами
![]() ,
,
де (х1;у1;z1) і (х2;у2;z2) – координати точок А1 і А2, що є кінцями відрізка.
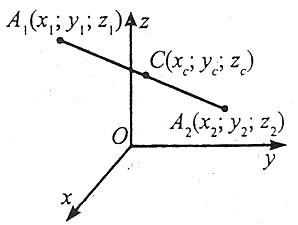
Приклад 3. Знайдіть координати точки С – середини відрізка АВ, якщо А(1;2;3), В(-3;2;1).
Розв’язання
Оскільки А(1;2;3), В(-3;2;1) і АС=СВ, то
![]() .
.
Отже, С(-1;2;2).
Відповідь: С(-1;2;2).
4. Рівняння фігури
Рівнянням фігури в декартових координатах у просторі називається рівняння із трьома невідомими х, у, z, які задовольняють координати будь-якої точки фігури, і тільки вони.
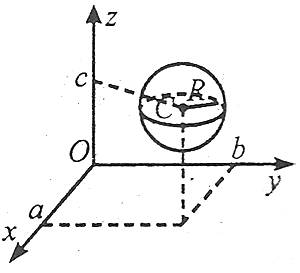
Рівняння сфери
Якщо в просторі задано деяку точку з координатами С(а,b,c), що є центром сфери, а також радіус R, то рівняння сфери має вигляд
![]() .
.
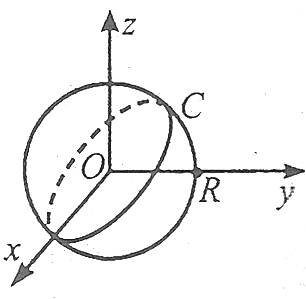
Якщо центром сфери є початок координат, то маємо
![]() .
.
Приклад 4. Складіть рівняння сфери з центром в точці В(1;1;3), якщо відомо, що сфера проходить через точку М(2;0;-1).
Розв’язання
Знайдемо радіус R сфери
![]() .
.
Ураховуючи, що центр сфери міститься в точці В(1;1;3), а радіус R сфери дорівнює ![]() , матимемо рівняння сфери
, матимемо рівняння сфери
![]() .
.
Відповідь: ![]() .
.