Вектори у просторі
Вектори у просторі
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Геометрія. |
| Книга: | Вектори у просторі |
| Надруковано: | Гість |
| Дата: | Saturday 24 May 2025 10:06 PM |
1. Координати вектора. Довжина вектора
1. Координати вектора
Координати вектора ![]() , що має початок в точці А і кінець в точці В, дорівнюють різниці відповідних координат точок В і А.
, що має початок в точці А і кінець в точці В, дорівнюють різниці відповідних координат точок В і А.
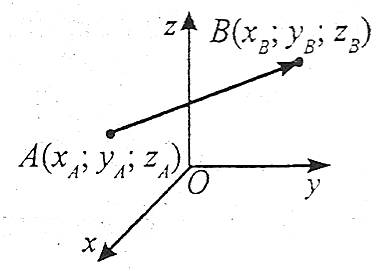
Координати вектора у просторі
Якщо початком вектора є точка А(хА;уА;zA), а кінцем – точка В(хВ;уВ;zB), то
![]()
2. Довжина вектора
Довжина вектора (абсолютна величина, або модуль) – довжина відрізка, що зображує вектор. Позначення: ![]() .
.
Довжина вектора у просторі
Якщо є вектор![]() , то
, то![]() =
= ![]() , де
, де ![]() – модуль вектора,
– модуль вектора, ![]() – його координати.
– його координати.
Одиничним називається вектор ![]() , у якого
, у якого ![]() .
.
Нульовим називається вектор![]() \, у якого початок і кінець збігаються. Нульовий вектор не має визначеного напрямку, а його модуль дорівнює нулю.
\, у якого початок і кінець збігаються. Нульовий вектор не має визначеного напрямку, а його модуль дорівнює нулю.
Задача 1. Знайдіть координати і довжини векторів ![]() і
і![]() , якщо А(2;-3;-1), В(-4;-8;5), С(3;1;-2).
, якщо А(2;-3;-1), В(-4;-8;5), С(3;1;-2).
Розв’язання
![]() ( - 4 - 2; - 8 - ( - 3);5 - ( - 1)) =
( - 4 - 2; - 8 - ( - 3);5 - ( - 1)) = ![]() ( - 6; - 5;6)\];
( - 6; - 5;6)\];
![]() (3 - 2;1 - ( - 3); - 2 - ( - 1)) =
(3 - 2;1 - ( - 3); - 2 - ( - 1)) = ![]() (1;4; - 1)\];
(1;4; - 1)\];
![]() =
= ![]() ;
;
![]() =
= ![]() .
.
Відповідь:![]() ,
, ![]() ,
,![]() \,
\, ![]() .
.
Рівність векторів у просторі
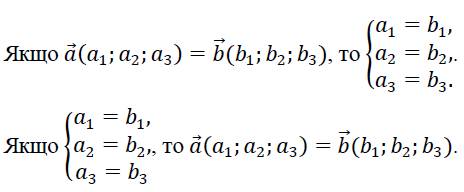
Протилежні вектори у просторі
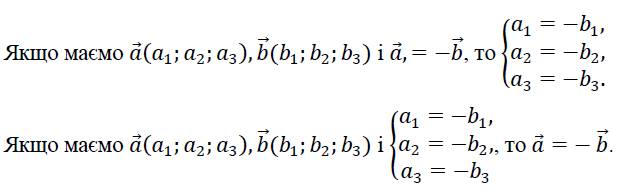
2. Дії з векторами у просторі
Для трьох векторів (ОА, ОС і ОО1), які не лежать в одній площині й мають спільний початком (О), їхня сума зображується діагоналлю паралелепіпеда (ОВ1), побудованого на цих векторах, причому початок вектора-суми збігається з початком цих векторів.
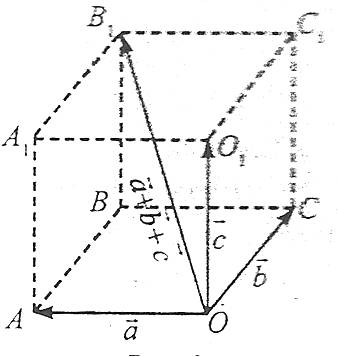
Координати вектора-суми векторів дорівнюють сумі відповідних координат даних векторів.
Сума векторів у просторі
![]()
Різниця векторів у просторі
![]()
Множення вектора на число у просторі
![]()
Задача 2. Задано вектори ![]() .
.
Знайдіть координати векторів ![]() .
.
Розв’язання
![]() ;
;
![]() ;
;
![]()
Відповідь: ![]() .
.
3. Колінеарність векторів у просторі
Якщо є вектори ![]() і вони колінеарні, то
і вони колінеарні, то ![]() .
.
Якщо є вектори ![]() , то
, то ![]() – колінеарні вектори.
– колінеарні вектори.
Задача 3. Знайдіть значення m і n, при яких вектори ![]() колінеарні.
колінеарні.
Розв’язання
У колінеарних векторів координати пропорційні, звідси ![]() . Маємо два рівняння:
. Маємо два рівняння:
1) ![]() ;
;
2) ![]() .
.
Відповідь: m=1, n=-10.
4. Скалярний добуток двох векторів
Скалярним добутком двох векторів називається число, яке дорівнює сумі добутків відповідних координат цих векторів. Позначення таке саме, як і для добутку чисел, – ![]() .
.
Скалярний добуток двох векторів на площині
Якщо є вектори![]() , то
, то ![]() .
.
Теорема. Скалярний добуток двох векторів дорівнює добутку довжин цих векторів на косинус кута між ними.
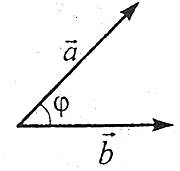
Отже, ![]() .
.
Задача 4. Знайдіть кут між векторами![]() і
і ![]() .
.
Розв’язання
Скористаємося формулою
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
тоді ![]() .
.
Звідси ![]() .
.
Відповідь: ![]() .
.
5. Ознака перпендикулярності векторів
Якщо вектори перпендикулярні, то їхній скалярний добуток дорівнює нулю.
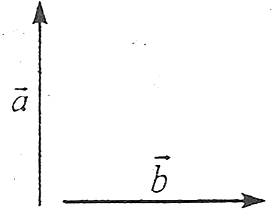
І навпаки, якщо скалярний добуток відмінних від нуля векторів дорівнює нулю, то вектори перпендикулярні.
Задача 5. При якому значенні р вектори ![]() і
і ![]() взаємно перпендикулярні?
взаємно перпендикулярні?
Розв’язання
Два ненульові вектори перпендикулярні тоді і тільки тоді, коли їхній скалярний добуток дорівнює нулю.
![]() , тоді
, тоді ![]() . Звідси р=5.
. Звідси р=5.
Відповідь: р=5.