Степеневі функції та їх властивості. Ірраціональні рівняння, нерівності та їх системи
Степеневі функції та їх властивості. Ірраціональні рівняння, нерівності та їх системи
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | Степеневі функції та їх властивості. Ірраціональні рівняння, нерівності та їх системи |
| Надруковано: | Гість |
| Дата: | Sunday 22 June 2025 1:10 PM |
1. Степенева функція
Степеневою функцією називається функція виду  , де р – стале дійсне число, а х (основа) – змінна. Властивості та графіки степеневих функцій подано в таблиці 1.
, де р – стале дійсне число, а х (основа) – змінна. Властивості та графіки степеневих функцій подано в таблиці 1.
Таблиця 1.
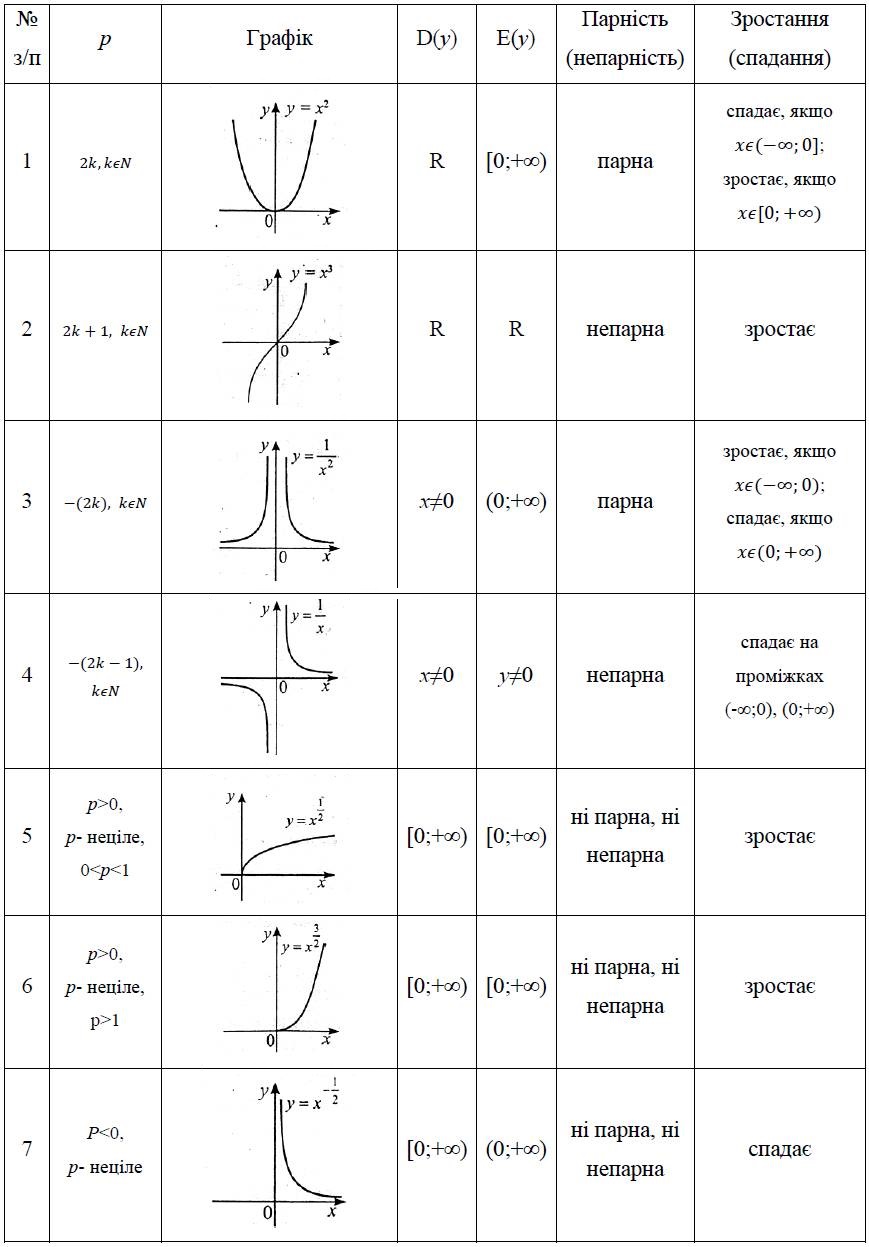
При знаходженні області визначення слід памятати, якщо функція має вигляд  , то:
, то:
1) якщо α – натуральне число, то D(y)=R;
2) якщо α – ціле від’ємне число або нуль, то  ;
;
3) якщо α – додатне неціле число, то D(y)=[0;+∞);
4) якщо α – від’ємне неціле число, то D(y)=(0;+∞).
Властивості та графіки функції ![y = \sqrt[n]{x} y = \sqrt[n]{x}](http://zno.academia.in.ua/filter/tex/pix.php/d18c5d94109a43bc623c0e24574fb854.gif) подано в таблиці 2.
подано в таблиці 2.
Таблиця 2.

Якщо функція має вигляд ![y = \sqrt[{2k}]{{f(x)}},k \in N y = \sqrt[{2k}]{{f(x)}},k \in N](http://zno.academia.in.ua/filter/tex/pix.php/00241865a9351a8aeb4889d099df1ad4.gif) , то слід вважати f(x)≥0 (арифметичний корінь парного степеня існує тільки з невід’ємних чисел).
, то слід вважати f(x)≥0 (арифметичний корінь парного степеня існує тільки з невід’ємних чисел).
2. Ірраціональні рівняння
Рівняння, у яких під знаком кореня міститься змінна (невідома), називають ірраціональними.
Наприклад: ![\sqrt[3]{{x - 2}} + 3 = 0,\;\sqrt x = \sqrt x + x \sqrt[3]{{x - 2}} + 3 = 0,\;\sqrt x = \sqrt x + x](http://zno.academia.in.ua/filter/tex/pix.php/3e2c71a77125f831fdd38252276d3713.gif) - ірраціональні рівняння.
- ірраціональні рівняння.
Розв’язування ірраціональних рівнянь ґрунтується на приведенні їх за допомогою деяких перетворень до раціонального рівняння. Як правило, це досягається піднесенням обох частин ірраціонального рівняння до одного і того самого степеня (інколи кілька разів).
При піднесенні обох частин рівняння до парного степеня одержане рівняння може мати корені, що не задовольняють даному рівнянню. Такі корені називаються сторонніми для даного рівняння. (Це відбувається тому, що з рівності парних степенів двох чисел не випливає рівність цих чисел.)
Тому слід обов’язково робити перевірку одержаних коренів.
Приклад 1. Розв’яжіть рівняння  .
.
Розв’язання
Рівняння  не має коренів, оскільки радикал із парним показником
не має коренів, оскільки радикал із парним показником  не може бути від’ємним.
не може бути від’ємним.
Приклад 2. Розв’яжіть рівняння  .
.
Розв’язання
Отже, х=3 сторонній корінь.
Відповідь: 2.
3. Ірраціональні нерівності
Для розв’язання ірраціональних нерівностей використовуємо узагальнений метод інтервалів. Розв’язком нерівності f(x)>0 (f(x)<0) можуть бути тільки числа, що входять в область визначення функції y=f(x). Розв’язком нерівності f(x)>0 є ті інтервали області визначення y=f(x), де ця функція є додатною. З’ясуємо яким чином довільна функція може змінити свій знак.
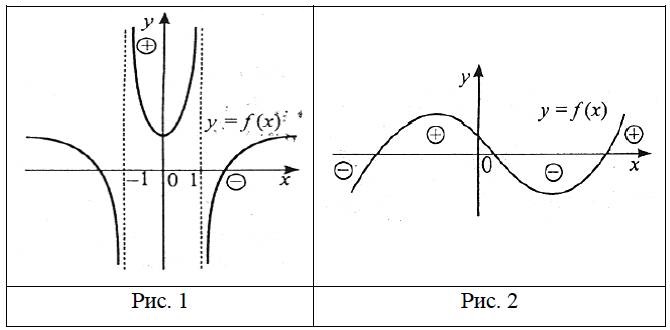
На рис. 1 і 2 зображено графіки двох функцій. На рис. 1 графік розривається в точках х=-1 та х=1 і знак функції змінюється при переході через точки -1 та 1. На рис. 2 знак функції змінюється при переході графіка з нижньої півплощини у верхню (і навпаки), тобто в тих точках, де графік перетинає вісь ОХ. На осі ОХ значення функції дорівнює нулю, тому значення аргументу, при яких функція дорівнює 0, називають нулями функції.
Отже, будь-яка функція може змінювати свій знак тільки в точках, де розривається графік функції, або в нулях.
Отже, щоб розв’язати нерівність f(x)>0 (f(x)<0), треба:
1) знайти область визначення функції y=f(x). (Коли ми знаходимо область визначення функції, то при цьому виділяються і точки, у яких розривається графік функції.);
2) знайти нулі функції (розв’язати рівняння f(x)=0);
3) на координатній прямій позначити нулі функції на області її визначення і визначити знак функції на кожному інтервалі, на які розбивають нулі функції область визначення (у кожному із цих інтервалів функція зберігає знак, і його можна визначити в будь-якій точці цього інтервалу);
4) записати відповідь (вибрати інтервали, де функція має потрібний знак).
![y = \sqrt[6]{{6 - x}} y = \sqrt[6]{{6 - x}}](http://zno.academia.in.ua/filter/tex/pix.php/f6e17229cda4ee5fc64d3048ab978879.gif)




