Приклади розв'язування завдань

     Завдання. Розв’яжіть рівняння $\sqrt[3]{{2x - 1}} = 3$.

Розв’язання

$\sqrt[3]{{2x - 1}} = 3;\;{(\sqrt[3]{{2x - 1}})^3} = {3^3};\;2x - 1 = 27;\;x = 14$.

     Відповідь: 14.

     Завдання. Розв’яжіть рівняння $\sqrt {2x - 6} = 5 - \sqrt {x + 4}$.

Розв’язання

     Обидві частини рівняння піднесемо до квадрата. Одержимо

$2x - 6 = 25 - 10\sqrt {x + 4} + x + 4$

або після перетворення $10\sqrt {x + 4} = 35 - x$.

     Знову піднесемо до квадрата обидві частини рівняння:

$100(x + 4) = {(35 - x)^2};\;100x + 400 = {x^2} - 70x + 1225;\;{x^2} - 170x + 825 = 0$.

     Звідси х₁=5, х₂=165.

     Перевірка:

1) $\sqrt {2 \cdot 5 - 6} = \sqrt 4 = 2,\quad 5 - \sqrt {5 + 4} = 5 - 3 = 2$;

2) $\sqrt {2 \cdot 165 - 6} \ne 5 - \sqrt {165 + 4}$.

     Отже, х=165 – сторонній корінь.

     Відповідь: 5.

     Завдання. Розв’яжіть рівняння ${x^2} + 3x - 18 + 4\sqrt {{x^2} + 3x - 6} = 0$.

Розв’язання

     Нехай $\sqrt {{x^2} + 3x - 6} = t,t \ge 0$, тоді ${x^2} + 3x - 18 = {t^2} - 12$ і дане рівняння стане таким: ${t^2} - 12 + 4t = 0$, звідси t₁=-6, t₂=2.

1) $\sqrt {{x^2} + 3x - 6} = - 6$ - розв’язків немає;

2) $\sqrt {{x^2} + 3x - 6} = 2,\;{x^2} + 3x - 6 = 4,\;{x^2} + 3x - 10 = 0$, звідси х=-5 або х=2.

     Перевірка показує, що -5 і 2 є коренями.

     Відповідь: -5, 2.

     Завдання. Розв’яжіть рівняння $\frac{{\sqrt {21 + x} + \sqrt {21 - x} }}{{\sqrt {21 + x} - \sqrt {21 - x} }} = \frac{{21}}{x}$.

Розв’язання

     Домножимо чисельник і знаменник дробу лівої частини рівняння на ${\sqrt {21 + x} + \sqrt {21 - x} }$. Тоді

$\frac{{x + 21 + 2\sqrt {21 + x} \cdot \sqrt {21 - x}  + 21 - x}}{{21 + x - 21 - x}} = \frac{{21}}{x};\;\frac{{21 + \sqrt {21 + x} \cdot \sqrt {21 - x} }}{x} = \frac{{21}}{x}$.

     Звідси 21-х=0 або 21+х=0.

1) 21-х=0, х=21;

2) 21+х=0, х=-21.

     Відповідь: 21; -21.

     Завдання. Розв’яжіть рівняння $\sqrt[3]{{8 - x}} + \sqrt[3]{{x + 1}} = 3$.

Розв’язання

      Піднесемо до куба обидві частини рівняння і одержимо:

$8 - x + 3{(\sqrt[3]{{8 - x}})^2}\sqrt[3]{{x + 1}} + 3\sqrt[3]{{8 - x}}{(\sqrt[3]{{x + 1}})^2} + x + 1 = 27$,

$3\sqrt[3]{{8 - x}}\sqrt[3]{{x + 1}}(\sqrt[3]{{8 - x}} + \sqrt[3]{{x + 1}}) = 18$.

     За умовою $\sqrt[3]{{8 - x}} + \sqrt[3]{{x + 1}} = 3$, тому

$3\sqrt[3]{{8 - x}}\sqrt[3]{{x + 1}} \cdot 3 = 18,\;\sqrt[3]{{(8 - x)(x + 1)}} = 2,\;{x^2} - 7x = 0$.

     Звідси х=0, х=7.

     Зробивши перевірку, впевнюємося, що обидва корені є коренями рівняння.

     Відповідь: 0; 7.

     Завдання. Розв’яжіть систему рівнянь

$\left\{ \begin{array}{l}\sqrt x + \sqrt y = 4,\\\sqrt x - \sqrt y = 2.\end{array} \right.$

Розв’язання

     Додавши почленно ліві та праві частини рівнянь, отримаємо $2\sqrt x = 6$. Звідси $\sqrt x = 3,\;x = 9$.

     Віднявши почленно ліві і праві частини рівнянь, отримаємо $2\sqrt y = 2$. Звідси $\sqrt y = 1,\;y = 1$.

     Відповідь: (9;1).

     Приклад 9. Розв’яжіть систему рівнянь

$\left\{ \begin{array}{l}\sqrt[4]{{x + y}} - \sqrt[4]{{x - y}} = 2,\\\sqrt {x + y} - \sqrt {x - y} = 8.\end{array} \right.$

Розв’язання

     Уведемо нові змінні: $\sqrt[4]{{x + y}} = a,\;\sqrt[4]{{x - y}} = b$.

     Ця система набуває вигляду

$\left\{ \begin{array}{l}a - b = 2,\\a2 - b2 = 8;\end{array} \right.\;\left\{ \begin{array}{l}a - b = 2,\\(a - b)(a + b) = 8;\end{array} \right.\;\left\{ \begin{array}{l}a - b = 2,\\2(a + b) = 8;\end{array} \right.\;\left\{ \begin{array}{l}a - b = 2,\\a + b = 4;\end{array} \right.\;\left\{ \begin{array}{l}2a = 6,\\2b = 2;\end{array} \right.\;\left\{ \begin{array}{l}a = 3,\\b = 1.\end{array} \right.$

     Повертаючись до цих змінних, отримаємо:

$\left\{ \begin{array}{l}\sqrt[4]{{x + y}} = 3,\\\sqrt[4]{{x - y}} = 1;\end{array} \right.\quad \left\{ \begin{array}{l}{(\sqrt[4]{{x + y}})^4} = {3^4},\\{(\sqrt[4]{{x - y}})^4} = {1^4};\end{array} \right.\quad \left\{ \begin{array}{l}x + y = 81,\\x - y = 1;\end{array} \right.\quad \left\{ \begin{array}{l}2x = 82;\\2y = 80;\end{array} \right.\quad \left\{ \begin{array}{l}x = 41;\\y = 40.\end{array} \right.$

     Перевірка:

$\left\{ \begin{array}{l}\sqrt[4]{{41 + 40}} - \sqrt[4]{{41 - 40}} = 3 - 1 = 2,\\\sqrt {41 + 40} - \sqrt {41 - 40} = 9 - 1 = 8.\end{array} \right.$

     Відповідь: (41;40).

     Завдання. Розв’яжіть нерівність $\sqrt {(x + 2)(x - 5)} < 8 - x$.

Розв’язання

     Приведемо нерівність до вигляду $\sqrt {(x + 2)(x - 5)} - 8 + x < 0$.

     Уведемо функцію $y = \sqrt {(x + 2)(x - 5)} - 8 + x$ і знайдемо х, при яких у<0. Для цього:

1)               знайдемо область визначення функції:

$(x + 2)(x - 5) \ge 0;\;D(y) = ( - \infty ; - 2] \cup [5; + \infty )$;

2)               знайдемо нулі функції:

$\sqrt {(x + 2)(x - 5)} - 8 + x = 0,\;\sqrt {(x + 2)(x - 5)} = 8 - x$,

$(x + 2)(x - 5) = 64 - 16x + {x^2},\;{x^2} - 3x - 10 = 64 - 16x + {x^2}$,

$13x = 74,\;x = 5\frac{9}{{13}}$.

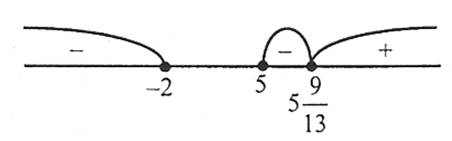
3)               наносимо нуль функції на область її визначення. Знаходимо знак функції на кожному з трьох інтервалів, на які розбивається область визначення нулем функції, і записуємо відповідь.

$f( - 3) = \sqrt {( - 3 + 2)( - 3 - 5)} - 8 - 3 = \sqrt 8 - 8 - 3 < 0$,

$f(5,5) = \sqrt {(5,5 + 2)(5,5 - 5)} - 8 + 5,5 = \sqrt {3,75} - 2,5 < 0$,

$f(6) = \sqrt {(6 + 2)(6 - 5)} - 8 + 6 = \sqrt 8 - 2 > 0$.

     Відповідь: $( - \infty ; - 2] \cup [5;5\frac{9}{{13}})$.