Приклади розв'язування завдань
Приклади розв'язування завдань
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | Приклади розв'язування завдань |
| Надруковано: | Гість |
| Дата: | Tuesday 1 July 2025 6:00 AM |
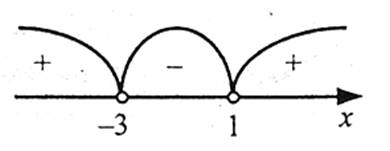
1. Приклад 1
Завдання. Розв’яжіть рівняння  .
.
Розв’язання
Оскільки  при всіх значення х, то рівняння коренів не має.
при всіх значення х, то рівняння коренів не має.
Відповідь: немає коренів.
7. Приклад 7
Завдання. Розв’яжіть систему рівнянь
Розв’язання
Отже,
є розв’язками системи.
Відповідь: (1;2), (2;1).
8. Приклад 8
Завдання. Розв’яжіть систему рівнянь
Розв’язання
Перемножимо і розділимо рівняння системи, тоді одержимо:
Відповідь: (2;1).
9. Приклад 9
Завдання. Розв’яжіть графічно нерівність  .
.
Розв’язання
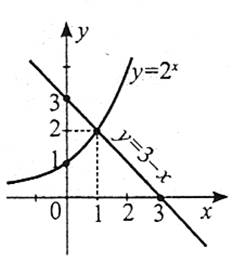
Із рисунка видно, що при х≤1. Отже, розв’язком нерівності є проміжок (-∞;1].
Відповідь: (-∞;1].