Приклади розв'язування завдань
Приклади розв'язування завдань
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | Приклади розв'язування завдань |
| Надруковано: | Гість |
| Дата: | Monday 19 May 2025 11:58 AM |
Приклад 2
Завдання. Розв’яжіть рівняння  .
.
Розв’язання
Із рівності логарифмів чисел випливає
Перевірка:
1) число -3 не є коренем даного рівняння, бо вираз  – не визначений;
– не визначений;
Відповідь: 2.
Приклад 3
Завдання. Розв’яжіть рівняння  .
.
Розв’язання
За означенням логарифма маємо
Перевірка:
1) Значення х=0 не є коренем даного рівняння, оскільки основа логарифма х+1 не повинна дорівнювати 1;
Відповідь: 2.
Приклад 4
Завдання. Розв’яжіть рівняння  .
.
Розв’язання
Позначимо  . Дане рівняння набуває вигляду:
. Дане рівняння набуває вигляду:
Перевірка:
Приклад 5
Завдання. Розв’яжіть рівняння  .
.
Розв’язання
Пропонеціюємо дану рівність і одержимо:
Перевірка:
1) Значення х=0 не є коренем рівняння, тому що вирази  і
і  не мають змісту при х=0;
не мають змісту при х=0;
Отже, х=4 – корінь.
Відповідь: 4.
Приклад 7
Завдання. Розв’яжіть рівняння  .
.
Розв’язання
Прологарифмуємо обидві частини рівності (х>0) і одержимо
Замінимо  . Рівняння набуває вигляду:
. Рівняння набуває вигляду:
Тоді:
Перевірка:
Відповідь: 100; 0,1.
Приклад 8
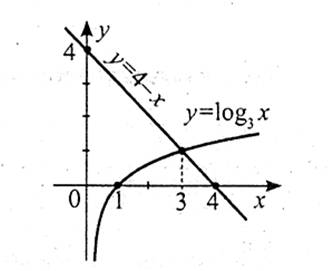
Завдання. Розв’яжіть рівняння  графічно.
графічно.
Розв’язання
В одній і тій самій системі координат побудуємо графіки функції  і
і  .
.
Абсциса точки перетину побудованих графіків дорівнює 1. Отже, х=1 – корінь даного рівняння.
Відповідь: 1.
Зауваження. Корінь цього рівняння легко знайти усно, однак треба пам’ятати, що в цьому випадку необхідно доводити той факт, що знайдений корінь єдиний.
Приклад 9
Завдання. Розв’яжіть систему рівнянь
Розв’язання
Тоді маємо:
Перевіркою впевнюємося, що (9;7), (7;9) – розв’язки системи.
Відповідь: (9;7), (7;9).
Приклад 10
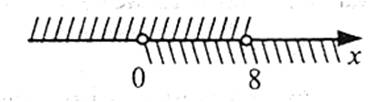
Завдання. Розв’яжіть нерівність  .
.
Розв’язання
Оскільки  , то запишемо дану нерівність у вигляді
, то запишемо дану нерівність у вигляді  . Оскільки функція
. Оскільки функція  зростаюча при х>0, то маємо
зростаюча при х>0, то маємо
Отже, 0<х<8.
Приклад 11
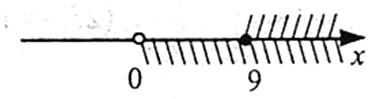
Завдання. Розв’яжіть нерівність  .
.
Розв’язання
Запишемо дану нерівність у вигляді  . Оскільки функція
. Оскільки функція  спадна при х>0, маємо
спадна при х>0, маємо
Отже, х≥9.
Приклад 12
Завдання. Розв’яжіть нерівність  .
.
Розв’язання
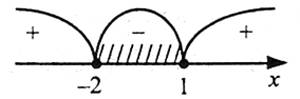
Одержана нерівність рівносильна системі
Розв’язком першої нерівності є  .
.
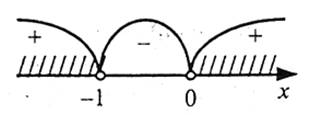
Розв’язком другої нерівності є [-2;1].
Приклад 13
Завдання. Розв’яжіть нерівність  .
.
Розв’язання
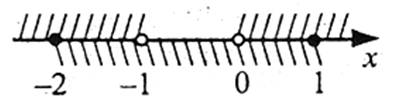
Нехай  , тоді отримаємо нерівність
, тоді отримаємо нерівність  . Розв’яжемо отриману нерівність методом інтервалів:
. Розв’яжемо отриману нерівність методом інтервалів:
Ураховуючи заміну, маємо:
Приклад 14
Завдання. Розв’яжіть нерівність  .
.
Розв’язання
Нехай lg x=y, тоді матимемо нерівність
Розв’яжемо отриману нерівність методом інтервалів
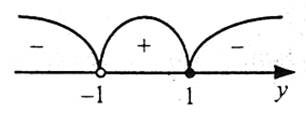
Ураховуючи заміну, одержимо -1<lg x≤1.
Тоді
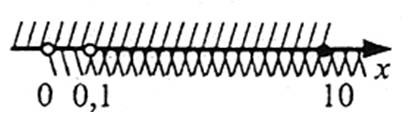
Відповідь: (0,1;10].
Приклад 15
Завдання. Розв’яжіть нерівність  .
.
Розв’язання
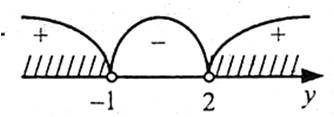
Нехай  , у>0. Область визначення функції у: х>0. Знайдемо нулі функції:
, у>0. Область визначення функції у: х>0. Знайдемо нулі функції:
Розіб’ємо область визначення функції не проміжки точками 2 і 1 і знайдемо знаки функції на утворених проміжках.
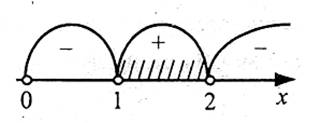
Відповідь: (1;2).
Приклад 16
Завдання. Розв’яжіть нерівність  .
.
Розв’язання
Нехай  і у<0. Область визначення функції знаходимо із системи:
і у<0. Область визначення функції знаходимо із системи:
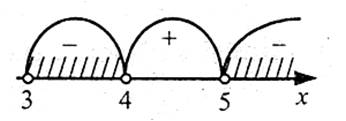
Знайдемо нулі функції:
Значення х=2 не входить в область визначення функції. Зробивши перевірку, переконуємося, що х=5 – нуль функції.
Розіб’ємо область визначення функції на проміжки точкою 5 та знайдемо знаки функції на утворених проміжках.





































![[ - 2; - 1) \cup (0;1] [ - 2; - 1) \cup (0;1]](http://zno.academia.in.ua/filter/tex/pix.php/0911e92f7a0d98b57f5e6c6af9c1cc5a.gif)





![y \in ( - 1;1] y \in ( - 1;1]](http://zno.academia.in.ua/filter/tex/pix.php/769d1edc86a01e99df52d08c8e5dd9c8.gif)

![x \in (0,1;10] x \in (0,1;10]](http://zno.academia.in.ua/filter/tex/pix.php/0b3bf30c010236f7e1f3d656d54fcef7.gif)