Похідна функції, її геометричний та механічний зміст
Похідна функції, її геометричний та механічний зміст
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | Похідна функції, її геометричний та механічний зміст |
| Надруковано: | Гість |
| Дата: | Thursday 3 July 2025 11:29 AM |
Означення похідної
Нехай задано функцію y=f(x) на деякому проміжку. Візьмемо довільну внутрішню точку x0 цього проміжку, надамо значенню х0 довільного приросту Δx (число Δх може бути як додатним, так і від’ємним), але такого, щоб точка х0+Δх належала даному проміжку.
Тоді
1) обчислимо в точці х0 приріст Δу=Δf(х0) функції:
3) знайдемо границю цього відношення за умови, що Δх→0, тобто:
Якщо дана границя існує, то її називають похідною функції y=f(x) у точці х0 і позначають  або
або  .
.
Похідною функції y=f(x) у точці х0 називають границю відношення приросту функції до приросту аргументу за умови, що приріст аргументу прямує до нуля, а границя існує, тобто
Із другого прикладу можна зробити висновок, що похідна лінійної функції – стала величина, яка дорівнює кутовому коефіцієнту прямої. Якщо у формулі  покласти k=0, b=C, де С – довільна стала, то одержимо, що
покласти k=0, b=C, де С – довільна стала, то одержимо, що  , тобто похідна сталої дорівнює нулю.
, тобто похідна сталої дорівнює нулю.
Якщо у формулі  покласти k=1, b=0, то одержимо
покласти k=1, b=0, то одержимо  .
.
Функцію, яка має похідну в точці х0, називають диференційованою в цій точці. Функцію, яка має похідну в кожній точці деякого проміжку, називають диференційованою на цьому проміжку. Операція знаходження похідної називається диференціюванням.
Нехай D1 – множина точок, у яких функція y=f(x) диференційована. Якщо кожному  поставити у відповідність число
поставити у відповідність число  , то одержимо нову функцію з областю визначення D1. Цю функцію позначають
, то одержимо нову функцію з областю визначення D1. Цю функцію позначають  :
:
Фізичний зміст похідної
Нехай матеріальна точка М рухається прямолінійно за законом s=f(t).
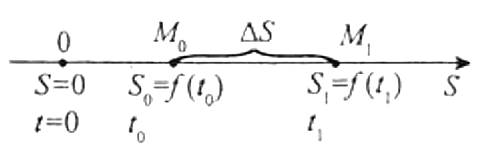
У момент t0 вона зайняла положення М0 і пройшла шлях s0=f(t0). Знайдемо швидкість точки в момент t0.
Припустимо, що за довільно вибраний проміжок часу Δt, починаючи з моменту t0, точка перемістилася на відстань Δs і зайняла положення М1.
Тоді t1=t0+Δt, s1=f(t1)=s0+Δs.
За проміжок часу Δt матеріальна точка проходить шлях
ΔS=f(t1)-f(t0)=f(t0+Δt)-f(t0).
Середня швидкість (vсер.) руху на проміжку М0М1 дорівнює
Ця величина дає лише приблизне уявлення про швидкість руху матеріальної точки на розглянутому проміжку. Вона буде точнішою, якщо проміжок Δt зменшуватиметься.
Таким чином, можна вважати, якщо Δt наближається до нуля, то середня швидкість  буде наближатися до швидкості в момент t0.
буде наближатися до швидкості в момент t0.
Миттєвою швидкістю точки, яка рухається прямолінійно, у момент t0 називають границею середньої швидкості за умови, що Δt наближається до нуля:
Числа Δt, Δs називають відповідно приростом часу і приростом шляху.
Отже, миттєвою швидкістю точки, яка рухається прямолінійно, є границя відношення приросту шляху Δs до відповідного приросту часу Δt, коли приріст часу наближається до нуля.
Порівнюючи одержані результати з означенням похідної, можна зробити висновок: якщо матеріальна точка рухається прямолінійно і її координата змінюється за законом s=s(t), то швидкість її руху v(t) у момент t дорівнює похідній  :
:
Геометричний зміст похідної
У курсі геометрії дотичною до кола називають пряму, яка лежить у площині кола і має з колом лише одну спільну точку. Таке означення дотичної не може бути перенесено на всі криві (парабола, синусоїда, гіпербола тощо).
Наприклад, вісь OY має тільки одну спільну точку з графіком функції y=x3, проте її не можна вважати дотичною до кубічної параболи в точці 0.
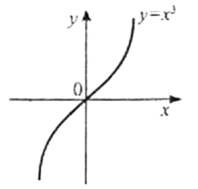
Пряма у=1 і синусоїда y=sin x мають безліч спільних точок, проте пряму у=1 вважають дотичною до синусоїди.
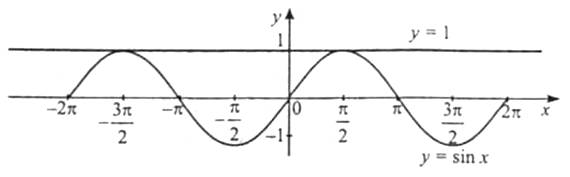
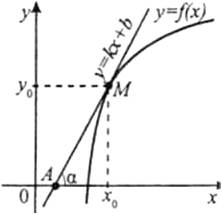
Для введення означення дотичної до кривої розглянемо функцію y=f(x) і її графік – криву лінію. Нехай точки А і М належать графіку функції y=f(x), проведемо січну АМ.
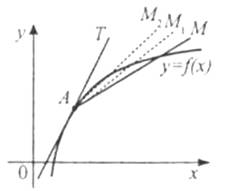
Зафіксуємо точку А. нехай точка М, рухаючись по кривій, наближається до точки А. при цьому січна АМ буде повертатися навколо точки А і в граничному положенні при наближенні точки М до точки А січна займе положення прямої АТ. Пряму АТ називають дотичною до даної кривої в точці А.
Дотичною АТ до графіка функції y=f(x) в точці А називають граничне положення січної АМ, коли точка М, рухаючись по кривій, наближається до точки А.
Слід мати на увазі, що не в усякій точці кривої можна провести до неї дотичну. На рис. зображено криву y=f(x), яка в точці А не має дотичної, бо якщо точка М буде наближатися до точки А по лівій частині кривої, то січна МА займе граничне положення AQ.
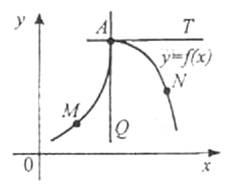
Якщо точка N буде наближатися по правій частині кривої, то січна NA займе граничне положення АТ. Одержуємо дві різні прямі AQ і АТ. Це означає, що в точці А до даної кривої дотичної не існує.
Поставимо задачу: провести дотичну до графіка функції y=f(x) у точці А(х0; у0).
Дотична – це пряма, а положення прямої , яка проходить через точку А(х0; у0) визначається кутовим коефіцієнтом прямої k=tg α, де α – кут між прямою і додатним напрямом осі ОХ.
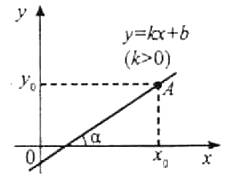
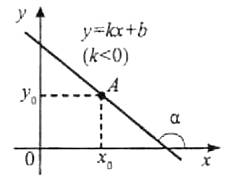
Отже, провести дотичну до графіка означає знайти число k.
Нехай у точці А(х0; у0) кривої y=f(x) існує дотична, визначимо кутовий коефіцієнт дотичної. Для цього:
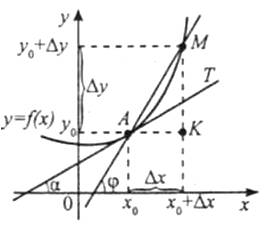
1) надамо аргументу х0 приросту Δх, одержимо нове значення аргументу х0+Δх;
2) знайдемо відповідний приріст функції Δy=f(x0+Δx)-f(x0);
3) знайдемо відношення  . Із трикутника АМК маємо
. Із трикутника АМК маємо  . Оскільки
. Оскільки  – куту нахилу січної АМ із додатним напрямом осі ОХ, то
– куту нахилу січної АМ із додатним напрямом осі ОХ, то  ;
;
4) якщо Δх→0, то Δу→0, і точка М буде переміщуватися по кривій, наближаючись до точки А.
При цьому січна АМ буде повертатися навколо точки А, а величина кута φ буде змінюватися зі зміною Δх. Граничним положенням січної АМ при Δх→0 буде дотична АТ, яка утворює з додатним напрямом осі ОХ деякий кут, величину якого позначимо через α.
Отже,  - кутовий коефіцієнт дотичної.
- кутовий коефіцієнт дотичної.
Порівнюючи одержані результати з означенням похідної, можна зробити висновок: значення похідної функції y=f(x) у точці х0 дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою х0:
Похідні елементарних функцій
Похідні елементарних функцій знаходять, користуючись таблицею похідних.
Таблиця
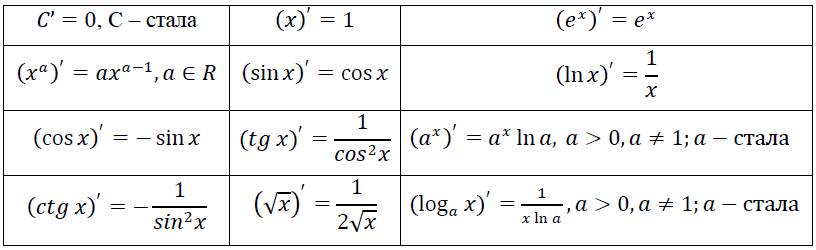
Похідна складеної функції
Похідна суми (різниці) двох функцій, кожна з яких має похідну, дорівнює сумі (різниці) похідних цих функцій:
Похідна добутку двох функцій, кожна з яких має похідну, дорівнює сумі добутків кожної функції на похідну другої функції:
Похідну частки частки двох функцій f(x) і g(x), кожна з яких має похідну і g(x)≠0, знаходять за формулою
Сталий множник можна виносити за знак похідної:
Наведені формули називають правилами диференціювання.
Приклад 1. Нехай треба обчислити за заданим значенням х значення функції у, яку задано формулою  .
.
Для цього спочатку треба обчислити за заданим значенням х значення  , а потім за значенням u обчислити
, а потім за значенням u обчислити  .
.
Отже, функція g ставить у відповідність числу х число u, а функція f – числу u число у. говорять, що у є складеною функцією з функцій g і f, і пишуть y=f(g(x)).
Функцію g(x) називають внутрішньою функцією, або проміжною змінною, функцію f(u) – зовнішньою функцією. Отже, щоб обчислити значення складеної функції y=f(g(x)) у довільній точці х, спочатку обчислюють значення u внутрішньої функції g, а потім f(u).
Приклад 2. Розглянемо функцію  . Вона є складеною з функцій u=cos x,
. Вона є складеною з функцій u=cos x,  , де cos х – внутрішня функція,
, де cos х – внутрішня функція,  – зовнішня функція.
– зовнішня функція.
Приклад 3. Запишіть складені функції f(g(x)) і g(f(x)), якщо f(x)=sin x,  .
.
Розв’язання
Складена функція y=f(g(x)) має проміжну змінну u=g(x). Тому при знаходженні похідної складеної функції ми будемо вказувати, по якій змінні взято похідну, використовуючи при цьому спеціальні позначення:
 - похідна функції у по аргументу х;
- похідна функції у по аргументу х;
 - похідна функції у по аргументу u;
- похідна функції у по аргументу u;
 - похідна функції u по аргументу х.
- похідна функції u по аргументу х.
Теорема
Похідну складеної функції y=f(g(x)) знаходять за формулою
де u=g(x), або похідна складеної функції дорівнює похідній зовнішньої функції по проміжній змінній, помноженій на похідну внутрішньої функції по основному аргументу.















