Похідна та її застосування
Похідна та її застосування
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | Похідна та її застосування |
| Надруковано: | Гість |
| Дата: | Friday 20 June 2025 5:55 AM |
Достатня умова зростання (спадання) функції на проміжку
Відомо, що функцію y=f(x) називають зростаючою на деякому проміжку, якщо для будь-яких х1 і х2, що належать проміжку, з умови х2>х1 випливає, що f(x2)>f(x1).
Дотична в кожній точці графіка зростаючої функції, утворює з додатним напрямом осі ОХ або гострий кут, або кут, що дорівнює нулю (в останньому випадку дотична є паралельною осі ОХ).
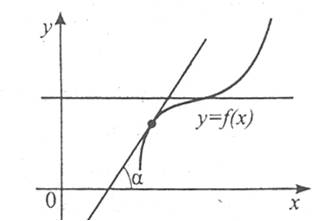
Виходячи з геометричного змісту похідної,  . Це означає, що похідна в кожній точці проміжку невід’ємна, тому для зростаючої функції f(x) виконується умова
. Це означає, що похідна в кожній точці проміжку невід’ємна, тому для зростаючої функції f(x) виконується умова
Функцію y=f(x) називають спадною на проміжку, якщо для будь-яких х1 і х2, що належать проміжку, з умови х2>х1 випливає, що f(x2)<f(x1). Дотична в кожній точці графіка спадної функції, утворює з віссю ОХ або тупий кут, або кут, що дорівнює нулю, тому для функції f(x), яка спадає на деякому проміжку, виконується умова
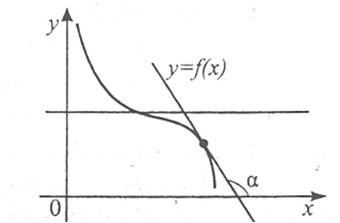
Одна й та сама функція може на одному проміжку області її визначення зростати, а на іншому – спадати. Характер поведінки функції на кожному із цих проміжків визначається знаком її похідної.
Отже, наочне уявлення дозволяє сформулювати властивості зростаючих та спадних функцій.
Якщо функція y=f(x) диференційована і зростає на деякому проміжку, то її похідна на цьому проміжку невід’ємна.
Якщо функція y=f(x) диференційована і спадає на деякому проміжку, то її похідна на цьому проміжку недодатна.
Проте для розв’язування задач особливо важливими є обернені твердження, які виражають ознаки зростання і спадання функції на проміжку. Нехай значення похідної функції y=f(x) додатні на деякому проміжку, тобто  . Оскільки
. Оскільки  , то з умови tg α>0 випливає, що дотичні, проведені до графіка функції в будь-якій точці цього інтервалу, утворюють гострі кути з додатним напрямом осі ОХ. У цьому випадку графік функції «піднімається» на заданому проміжку, тобто функція зростає.
, то з умови tg α>0 випливає, що дотичні, проведені до графіка функції в будь-якій точці цього інтервалу, утворюють гострі кути з додатним напрямом осі ОХ. У цьому випадку графік функції «піднімається» на заданому проміжку, тобто функція зростає.
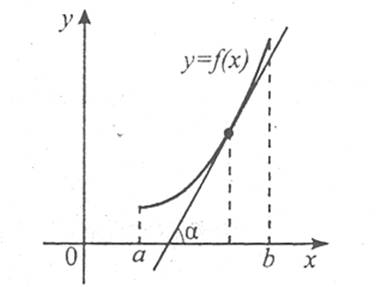
Якщо  на деякому проміжку, то кутовий коефіцієнт дотичної
на деякому проміжку, то кутовий коефіцієнт дотичної  до графіка функції y=f(x) від’ємний. Це означає, що дотична до графіка функції утворює з віссю ОХ тупий кут і графік функції на даному проміжку «опускається», тобто функція f(x) спадає.
до графіка функції y=f(x) від’ємний. Це означає, що дотична до графіка функції утворює з віссю ОХ тупий кут і графік функції на даному проміжку «опускається», тобто функція f(x) спадає.
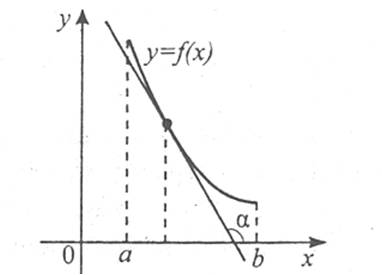
Якщо  на проміжку, то функція f(x) зростає на цьому проміжку.
на проміжку, то функція f(x) зростає на цьому проміжку.
Якщо  на проміжку, то функція f(x) спадає на цьому проміжку.
на проміжку, то функція f(x) спадає на цьому проміжку.
Ці два твердження називають ознаками зростання (спадання) функції на проміжку.
Проміжки зростання і спадання функції часто називають проміжками монотонності цієї функції.
Поняття екстремуму функції
При дослідженні поведінки функції в деякій точці зручно користуватися поняттям околу. Околом точки а називають будь-який інтервал, що містить цю точку.
Наприклад: інтервали (2; 5), (2,5; 3,5), (2,9; 3,1) – околи точки 3.
Розглянемо графік функції.
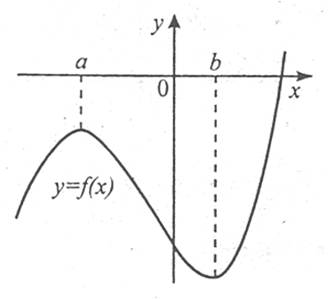
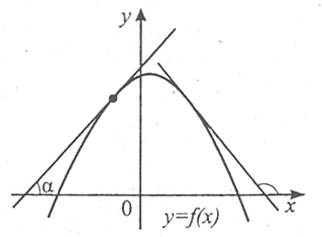
Як видно з рисунка, існує такий окіл точки х=а, що найбільше значення функції y=f(x) у цьому околі набуває в точці х=а. точку х=а називають точкою максимуму цієї функції.
Аналогічно точку х=b називають точкою мінімуму функції y=f(x), оскільки значення функції в цій точці найменше порівняно зі значеннями функції в деякому околі точки b.
Означення. Точка а з області визначення функції f(x) називається точкою максимуму цієї функції, якщо існує такий окіл точки а, що для всіх х≠а із цього околу виконується нерівність f(x)<f(a).
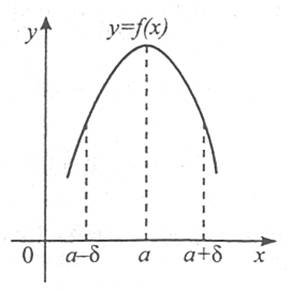
Означення. Точка b з області визначення функції f(x) називається точкою мінімуму цієї функції, якщо існує такий окіл точки b, що для всіх х≠b із цього околу виконується нерівність f(x)>f(b).
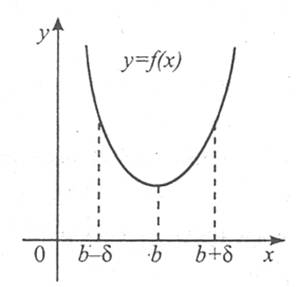
Точки максимуму і точки мінімуму називають точками екстремуму функції, а значення функції в цих точках – екстремумами функції (максимум і мінімум функції).
Точки максимуму позначають хmax, а точки мінімуму – хmin. Значення функції в цих точках, тобто максимуми і мінімуми, позначають відповідно уmаx і ymin.
Необхідна умова екстремуму
Розглянемо функцію y=f(x), яка визначена в деякому околі точки х0 і має похідну в цій точці.
Якщо х0 – точка екстремуму диференційованої функції y=f(x), то  .
.
Це твердження називають теоремою Ферма на честь французького математика П’єра Ферма (1601 – 1665).
Теорема Ферма має наочний геометричний зміст: у точці екстремуму дотична паралельна осі абсцис, і тому її кутовий коефіцієнт  дорівнює нулю.
дорівнює нулю.
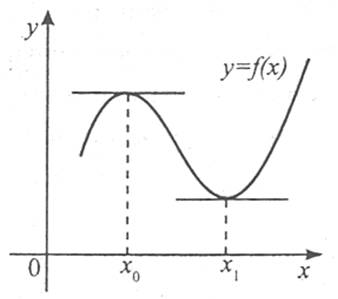
Наприклад: функція  має в точці х0=0 мінімум, її похідна
має в точці х0=0 мінімум, її похідна  .
.
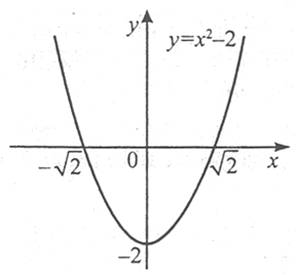
Функція  має максимум в точці х0=0,
має максимум в точці х0=0,  .
.
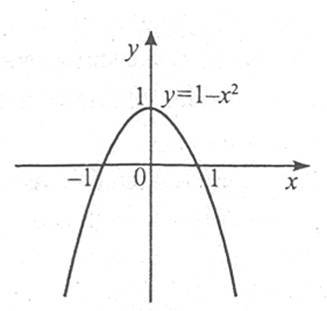
Слід зазначити, що якщо  , то х0 необов’язково є точкою екстремуму.
, то х0 необов’язково є точкою екстремуму.
Наприклад: якщо  , то
, то  і
і  . Проте точка х=0 не є точкою екстремуму, оскільки функція
. Проте точка х=0 не є точкою екстремуму, оскільки функція  зростає на всій числовій осі.
зростає на всій числовій осі.
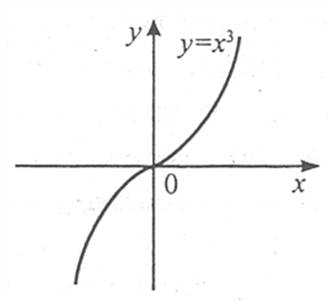
Отже, точки екстремуму диференційованої функції треба шукати тільки серед коренів рівняння  , але не завжди корінь рівняння
, але не завжди корінь рівняння  є точкою екстремуму.
є точкою екстремуму.
Внутрішні точки області визначення функції y=f(x), у яких похідна дорівнює нулю, називають стаціонарними. Отже, для того щоб точка х0 була точкою екстремуму, необхідно, щоб вона була стаціонарною.
Сформулюємо достатні умови для того, щоб стаціонарна точка була точкою екстремуму, тобто умови, при виконанні яких стаціонарна точка є точкою максимуму або мінімуму функції.
Якщо похідна ліворуч стаціонарної точки додатна, а праворуч – від’ємна, тобто при переході через цю точку похідна змінює знак із «+» на «-», то ця стаціонарна точка є точкою максимуму.
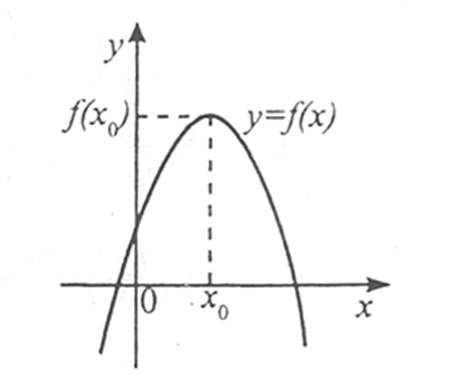
Дійсно, у цьому разі ліворуч стаціонарної точки функція зростає, а праворуч – спадає, отже, дана точка є точкою максимуму.
Якщо похідна ліворуч стаціонарної точки від’ємна, а праворуч – додатна, тобто при переході через стаціонарну точку похідна змінює знак із «-» на «+», то ця стаціонарна точка є точкою мінімуму.
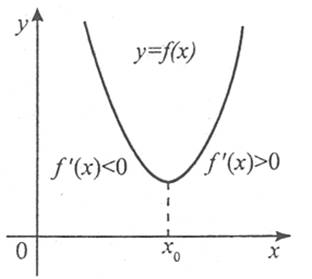
Якщо при переході через стаціонарну точку похідна не змінює знака, тобто ліворуч і праворуч від стаціонарної точки похідна додатна або від’ємна, то ця точка не є точкою екстремуму.
Найбільше і найменше значення функції на проміжку
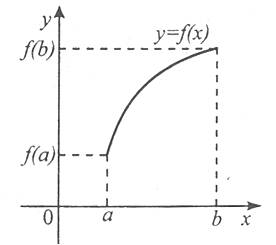
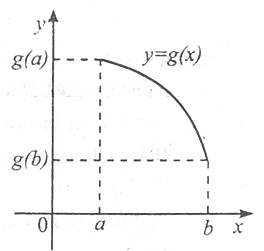
Розглянемо рис. 1 і 2, на яких зображено графіки функцій y=f(x) і y=g(x), заданих на відрізку [a; b].
|
|
|
|
Рис. 1 |
Рис. 2 |
Функція y=f(x) зростає, а функція y=g(x) спадає. На відрізку [a; b] найменше значення функції y=f(x) дорівнює f(a), а найменше значення функції y=g(x) дорівнює g(b). Відповідно найбільші значення цих функцій на даному відрізку дорівнюють f(b) та g(a). Отже, якщо функція непевна і зростає (спадає) на деякому відрізку, то найбільшого і найменшого значень функція набуває на кінцях цього відрізка.
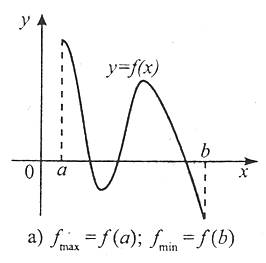
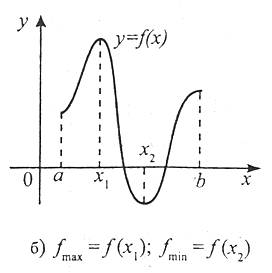
Розглянемо рис. 3, на якому зображено графіки трьох функцій. Аналіз цих графіків свідчить, що найбільше і найменше значення функцій неперервних і диференційованих на відрізку [a; b] досягаються цими функціями, або на кінцях відрізка, або в стаціонарних точках.
|
|
|
|
|
Рис. 3 |
||
Отже, неперервна і диференційована функція на заданому відрізку набуває найбільшого і найменшого значень у стаціонарних точках або на кінцях відрізка.