Застосування визначеного інтеграла
Застосування визначеного інтеграла
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | Застосування визначеного інтеграла |
| Надруковано: | Гість |
| Дата: | Monday 19 May 2025 11:20 AM |
Геометричний зміст визначеного інтеграла
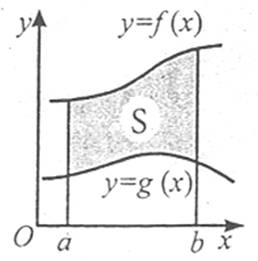
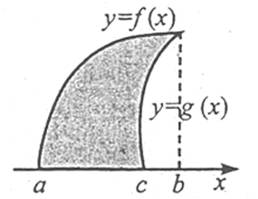
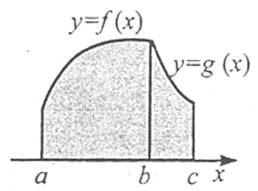
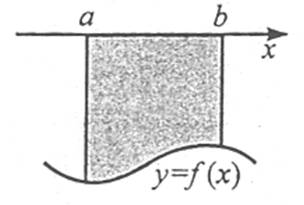
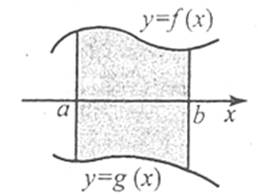
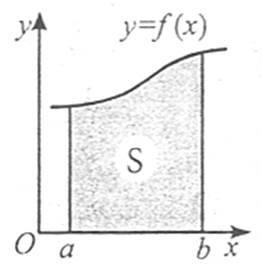
Площа S криволінійної трапеції (фігура, обмежена графіком неперервної додатної на проміжку [a; b] функції f(x), віссю Ох, та прямими х=а, х=b) обчислюється за формулою
![]() .
.
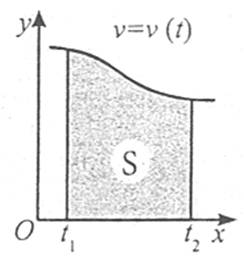
Фізичний зміст визначеного інтеграла
Під час прямолінійного руху переміщення s чисельно дорівнює
де v(t) – швидкість руху.

![x \in [a;b] x \in [a;b]](http://zno.academia.in.ua/filter/tex/pix.php/af2c40d55efcf03894d806afbf20ba84.gif)