Приклади розв'язування завдань
Приклади розв'язування завдань
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | Приклади розв'язування завдань |
| Надруковано: | Гість |
| Дата: | Monday 7 April 2025 11:49 AM |
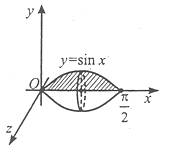
Приклад 1
Завдання. Обчисліть площу фігури, обмеженої лініями.
Розв’язання
Зобразимо схематично графіки даних функцій і заштрихуємо фігуру, площу якої необхідно знайти.
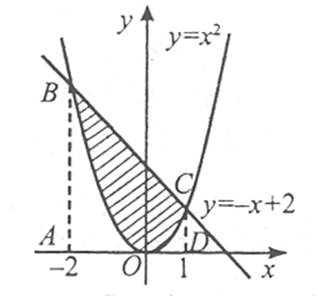
Для знаходження меж інтегрування розв’яжемо рівняння:
x2=−x+2;x2+x−2=0;x=−2 або x=1.
Тоді S=1∫−2((−x+2)−x2)dx=1∫−2(−x2−x+2)dx=(−x33−x22+2x)|1−2=
=−13−12+2−(83−2−4)=−93+1,5+6=7,5−3=4,5.
Відповідь: 4,5.