Початки теорії ймовірності
Початки теорії ймовірності
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | Початки теорії ймовірності |
| Надруковано: | Гість |
| Дата: | Tuesday 1 July 2025 8:44 AM |
Основні поняття
Подія – це явище, про яке можна сказати, що воно відбувається або не відбувається за певних умов. Події позначаються великими літерами латинського алфавіту: А, В, С,… Будь-яка подія відбувається внаслідок випробування (експерименту, досліду).
Випробування – це умови, за яких відбувається (чи не відбувається) подія.
Події розподіляються на випадкові, вірогідні та неможливі.
Випадковою називається подія, яка може відбутися або не відбутися внаслідок певного випробування.
Вірогідною називається подія, яка внаслідок даного випробування обов’язково відбудеться.
Неможливою називається подія, яка внаслідок даного випробування не може відбутися. Неможлива подія позначається символом .
Теорія ймовірностей – розділ математики, що вивчає закономірності випадкових подій.
Попарно несумісні події – це події, кожні дві з яких не можуть відбутися одночасно.
Рівноможливі події – події, кожна з яких не має ніяких переваг, щоб з’являтися частіше за іншу під час багаторазових випробувань, що проводяться за однакових умов.
Повною групою подій називається множина таких подій, коли в результаті кожного випробування обов’язково має відбутися хоча б одна з них.
Якщо події мають властивості: 1) утворювати повну групу подій; 2) бути несумісними; 3) бути рівно можливими, то такі події утворюють множину, яка називається простором елементарних подій.
Класичне означення ймовірності. Статистичне означення ймовірності
1. Класичне означення ймовірності
Відношення числа m елементарних подій, які сприяють події А, до загальної кількості n подій простору називається ймовірністю випадкової події А і позначається Р(А), тобто
![]() ,
,
де m – число подій, які сприяють події А, n – число подій простору елементарних подій (0≤m≤n).
Імовірність вірогідної події дорівнює 1, імовірність неможливої події дорівнює 0, а ймовірність Р(А) випадкової події А задовольняє умову 0<Р(А)<1.
Наприклад. Імовірність того, що при киданні двох монет випаде два герби, дорівнює , бо простір елементарних подій такий: А1 – випали два герби; А2 – випали герб і число; А3 – випали число і герб; А4 – випали два числа, а шуканій події сприяє лише одна подія – А1.
2. Статистичне означення ймовірності
Нехай n – кількість усіх випробувань в окремій серії випробувань, а m – кількість тих випробувань, у яких відбулася подія А.
Статистичною ймовірністю події А називається границя, до якої наближається відносна частота ![]() події А при необмеженому збільшенні числа всіх випробувань, тобто
події А при необмеженому збільшенні числа всіх випробувань, тобто
![]()
Операції над подіями.Теорема про ймовірність суми подій. Теорема про ймовірність добутку подій
1. Операції над подіями
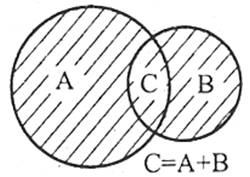
Сумою двох подій А і В називається подія , що полягає у здійсненні під час одиничного випробування або події А, або події В, або обох подій А і В одночасно (позначається С=А+В, або ![]() .
.
Подія ![]() називається протилежною події А, якщо вона відбувається тоді і тільки тоді, коли подія А не відбувається.
називається протилежною події А, якщо вона відбувається тоді і тільки тоді, коли подія А не відбувається.
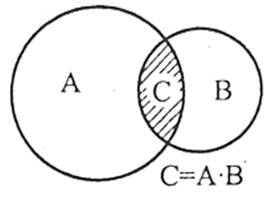
Добутком двох подій А і В називається подія С, яка полягає в одночасному здійсненні обох подій А і В під час одиничного випробування (позначається ![]() або
або ![]() .
.
2. Теорема про ймовірність суми подій
Імовірність суми двох несумісних подій А і В дорівнює сумі ймовірностей цих подій. Якщо ![]() , то Р(А+В)=Р(А)+Р(В).
, то Р(А+В)=Р(А)+Р(В).
Наприклад. Якщо спортсмен стріляє по мішені, яка розділена на 2 частини, і ймовірність попадання в першу частину дорівнює 0,45, а в другу – 0,35, то йовірність попадання в мішень становитиме 0,45+0,35=0,8.
Із теореми випливають наслідки.
Наслідок 1. Сума ймовірностей подій А1,А2,…,An, які утворюють повну групу і попарно несумісні, дорівнює 1
Р(А1)+Р(А2)+…+Р(Аn)=1.
Наслідок 2. Сума ймовірностей протилежних подій дорівнює 1
![]() .
.
3. Теорема про ймовірність добутку подій
Дві події називаються незалежними, якщо ймовірність появи однієї з них не залежить від того, відбулася інша подія чи ні.
Імовірність добутку двох незалежних подій А і В дорівнює добутку ймовірностей цих подій, тобто ![]() .
.
Якщо подія А1, А2, …Аn незалежні, то ймовірність здійснення принаймні однієї з них С може бути виражена через імовірність цих подій формулою
![]() .
.
Незалежні випробування. Схема Бернуллі. Закон великих чесел
1. Незалежні випробування. Схема Бернуллі
Взаємно незалежними випробуваннями називаються такі випробування, у яких імовірність результату кожного з них не залежить від того, які результати має чи матиме решта випробувань.
Багато задач у теорії ймовірностей зводяться до такої схеми, яка називається схемою Бернуллі: відбувається n незалежних випробувань, у кожному з яких подія А може настати чи не настати. Імовірність того, що випадкова подія А в кожному випробуванні відбувається, однакова і дорівнює p, а ймовірність того, що не відбувається, q=1-p. Треба знайти Рm,n того, що подія А настане m разів у цих n випробуваннях. Шукану ймовірність можна обчислити за формулою Бернуллі
![]() .
.
2. Закон великих чесел
Теорема Бернуллі. Якщо в ряді випробувань імовірність деякої події залишається для кожного випробування сталою і дорівнює р, то при достатньо великій кількості випробувань практично вірогідно, що частота ![]() появи події від її ймовірності менше, ніж яке завгодно мале число
появи події від її ймовірності менше, ніж яке завгодно мале число ![]() .
.