Вступ до статистики
Вступ до статистики
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | Вступ до статистики |
| Надруковано: | Гість |
| Дата: | Tuesday 1 July 2025 3:15 AM |
Поняття про статистику
Статистика – наука, що збирає, обробляє і вивчає різні дані, пов’язані з масовими явищами, процесами, подіями.
Математична статистика – розділ математики, присвячений математичним методам систематизації, обробки та дослідження статистичних даних для наукових і практичних висновків.
Статистичне спостереження – це спланований, науково-організований збір масових даних про соціально-економічні явища та процеси.
Найпоширенішим серед видів статистичних спостережень є вибіркове. У процесі вибіркового спостереження вивчається лише частина сукупності, відібрана спеціальним методом, яка називається вибіркою. Усю сукупність, із якої роблять вибірку, називають генеральною сукупністю. Число об’єктів генеральної сукупності й вибірки відповідно називають обсягом генеральної сукупності й обсягом вибірки.
Нехай із генеральної сукупності зроблено вибірку, причому х1 спостерігалося n1 разів, х2 – n2 разів, х3 – n3разів, xm – nm разів і n1+n2+n3+…+nm=N – обсяг вибірки. Значення х1, х2, х3,…xm називаються варіантами, послідовність варіант, записаних у зростаючому (спадному) порядку, – варіаційним рядом. Числа спостережень n1,n2,n3,…nm називають частотами, а їх відношення до обсягу вибірки ![]() – відносними частотами. Відзначимо, що сума відносних частот дорівнює 1:
– відносними частотами. Відзначимо, що сума відносних частот дорівнює 1:
![]()
Статистичним рядом розподілу вибірки називається перелік варіант і відповідних їм частот або відносних частот.
Статистичний розподіл можна задати у вигляді послідовності інтервалів і відповідних їм частот.
Статистичним рядом розподілу вибірки називається перелік варіант і відповідних їм частот або відносних частот.
Статистичний розподіл можна задати у вигляді послідовності інтервалів і відповідних їм частот.
Наприклад. Перейти від частот до відносних частот у такому розподілі вибірки обсягом N=20.
|
Варіанта хі |
2 |
6 |
12 |
|
Частота nі |
3 |
10 |
7 |
Розв’язання
Знайдемо відносні частоти:
![]() .
.
Тому одержуємо такий розподіл:
|
Варіанта хі |
2 |
6 |
12 |
|
Відносна частота рі |
0,15 |
0,50 |
0,35 |
Для графічного зображення статистичного розподілу використовують полігони і гістограми.
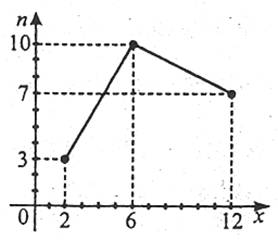
Для побудови полігону на осі ОХ відкладають значення варіант хі, на осі ординат – значення частот ni. Точки (хі;ni) з’єднують відрізками прямих і одержують полігон частот.
Наприклад 2. Побудувати полігон частот та полігон відносних частот статистичного розподілу з прикладу 1.
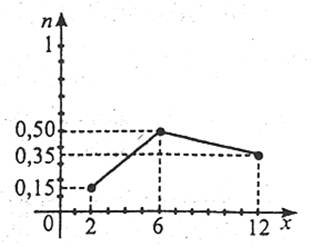
На мал. 1 побудовано полігон частот, а на мал. 2 – полігон відносних частот. У випадку інтервального розподілу доцільно побудувати гістограму, для чого інтервал, у якому містяться всі значення ознаки, яка спостерігається, розбивають на кілька інтервалів довжиною h і знаходять для кожного інтервалу ni – суму частот варіант, які попали в і-й інтервал.
|
|
|
|
Мал. 1 |
Мал. 2 |
Гістограмою частот називають східчасту фігуру, яка складається з прямокутників, основами яких є інтервали довжиною h, а висота дорівнює відношенню ![]() . Площа і-го прямокутника дорівнює
. Площа і-го прямокутника дорівнює![]() .
.
Отже, площа гістограми дорівнює сумі всіх частот, тобто обсягу вибірки.
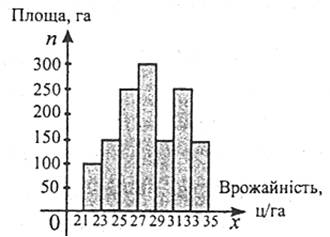
На мал. 3 подано гістограму за даними табл. 1.
Таблиця 1
|
Врожайність (ц/га) |
21 – 23 |
23 – 25 |
25 – 27 |
27 – 29 |
29 – 31 |
31 – 33 |
33 – 35 |
|
Площа (га) |
100 |
150 |
250 |
300 |
150 |
250 |
150 |
|
|
|
Мал. 3 |
Центральні тенденції вибірки
Вибірка характеризується центральними тенденціями: середнім значенням, модою і медіаною.
Середнім значенням вибірки називається середнє арифметичне всіх її значень:
![]() або
або ![]() .
.
Мода вибірки – те її значення, яке трапляється найчастіше (позначається М0).
Медіана вибірки – це число, яке ділить навпіл упорядковану сукупність усіх значень вибірки, тобто середня величина змінюваної ознаки, яка містить в середині ряду, розміщеного в порядку зростання або спадання ознаки (позначається Ме). Якщо кількість чисел у ряду парна, то медіана – середнє арифметичне двох чисел, що стоять посередині.
Середні значення
Статистика оперує такими середніми значеннями: середнє арифметичне, середнє квадратичне, середнє геометричне.
Відхиленням значення хі від середнього значення ![]() називається різниця
називається різниця![]() .
.
У статистиці користуються показником – середнє квадратичне відхилення, яке знаходять так: усі відхилення підносять до квадрата; знаходять середнє арифметичне цих квадратів; зі знайденого середнього арифметичного добувають квадратний корінь. Середнє квадратичне відхилення позначають грецькою буквою σ:
![]() .
.
У статистиці ![]() називають дисперсією.
називають дисперсією.
Середнє геометричне n додатних чисел ![]() визначається за формулою
визначається за формулою
![]() \.
\.
Якщо вибірку задано статистичним рядом, то
![]() або
або ![]()
![]() або
або ![]()