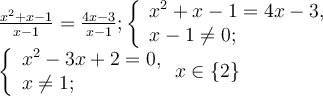Загальні методи розв'язування рівнянь, нерівностей та їх систем
Загальні методи розв'язування рівнянь, нерівностей та їх систем
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | Загальні методи розв'язування рівнянь, нерівностей та їх систем |
| Надруковано: | Гість |
| Дата: | Tuesday 1 July 2025 6:02 AM |
Рівносильні рівняння. Системи і сукупності рівнянь з однією змінною
1. Рівносильні рівняння
Два рівняння називаються рівносильними, якщо вони мають одні й ті самі корені або не мають їх зовсім. Знак рівносильності рівнянь – ![]() .
.
Наприклад:
1) ![]() , оскільки вони мають корінь х=2;
, оскільки вони мають корінь х=2;
2) ![]() .
.
2. Системи і сукупності рівнянь з однією змінною
Система рівнянь – це рівняння, відносно яких ставиться задача знайти їхні спільні корені. Знак системи – {.
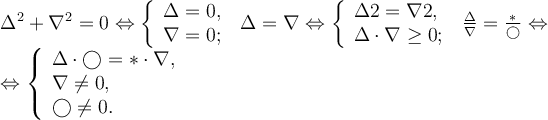
Наприклад:
![]()
Сукупність рівнянь – це рівняння, відносно яких ставиться задача знайти всі їхні корені. Знак сукупності – [.
![]()
Наприклад:
![]()
Методи розв’язування рівнянь
Розкладання на множники
Добуток кількох множників дорівнює нулю, якщо хоча б один із них дорівнює нулю, а останні при цьому існують.
Наприклад:
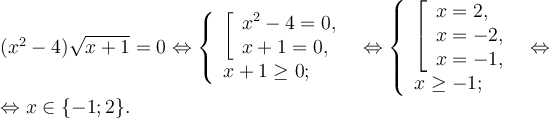
Заміна змінних
Наприклад: ![]()
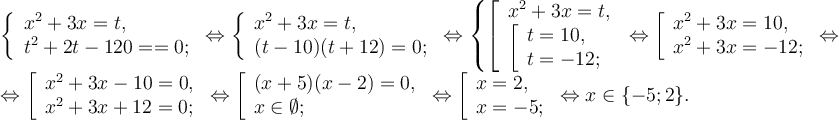
Порівняння обох частин рівняння за величиною
Наприклад: ![]() .
.
Оскільки ![]() , то
, то
![]()
Використання однорідності
![]()
Наприклад: ![]() .
.
Нехай ![]() , тоді
, тоді
![]() або
або ![]() .
.
Тоді
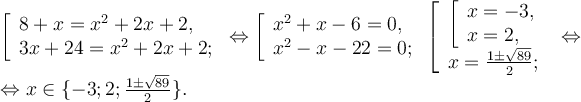
Використання монотонності
Наприклад: ![]() .
.
Функція ![]() спадна,
спадна, ![]() . Отже, х=2 – єдиний корінь.
. Отже, х=2 – єдиний корінь.
Графічний метод
Щоб графічно розв’язати рівняння f(x)=g(x), треба побудувати графіки функцій y=f(x) і y=g(x) і знайти абсциси точок їх перетину.
Наприклад: ![]() .
.
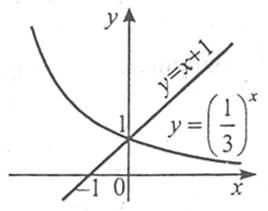
Відповідь: х=0.
Нерівносильні перетворення
|
Можуть призвести до втрати коренів |
|
|
Неправильне розв’язування:
Втрачено корінь х=0. |
Правильне розв’язування
|
|
Можуть призвести до появи сторонніх коренів |
|
|
Неправильне розв’язування
Корінь х=1 – сторонній |
Правильне розв’язування
|
Методи розв’язання нерівностей
Метод інтервалів
Щоб розв’язати нерівність ![]() , де
, де ![]() , де
, де ![]() – різні числа, треба:
– різні числа, треба:
- зобразити
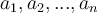 на координатній прямій (ці числа, розташовані у порядку зростання, розділяють пряму на проміжків, на яких функція f(x) зберігає свій знак);
на координатній прямій (ці числа, розташовані у порядку зростання, розділяють пряму на проміжків, на яких функція f(x) зберігає свій знак); - визначити знаки функції f(x) на кожному проміжку;
- записати відповідь.
Наприклад: ![]() .
.
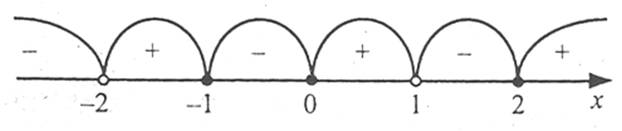
![]() .
.
Відповідь: ![]() .
.
Узагальнений метод інтервалів
Щоб розв’язати нерівність ![]() , треба:
, треба:
- знайти область визначення функції у=f(x);
- знайти нулі функції (f(x)=0);
- на координатній прямій позначити нулі функції і визначити знак функції на кожному проміжку, на які розбивають нулі функції область визначення;
- записати відповідь (вибрати ті інтервали, де функція має потрібний знак).
Графічний метод
Щоб розв’язати нерівність f(x)>g(x), треба побудувати графіки функцій y=f(x), y=g(x) і вибрати ті проміжки осі абсцис, на яких графік функції y=f(x)розташований вище графіка функції y=g(x).
Щоб розв’язати нерівність f(x)<g(x), треба побудувати графіки функцій y=f(x), y=g(x) і вибрати ті проміжки осі абсцис, на яких графік функції y=f(x)розташований нижче графіка функції y=g(x).
Наприклад: ![]() .
.
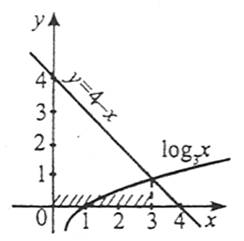
Відповідь:![]() .
.
Методи розв’язування систем рівнянь
Правило переходу до совокупності
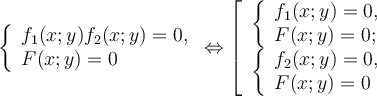
Правило додавання
![]()
Правило підстановки
![]()
Зведення системи рівнянь до об’єднання простіших систем
Наприклад: Розв’яжіть систему
![]()
Розв’язання
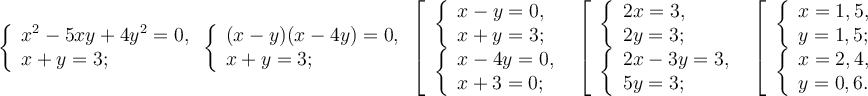
Відповідь: (1,5; 1,5), (2,4; 0,6).
Спосіб уведення нових змінних
Наприклад: Розв’яжіть систему
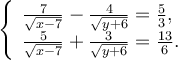
Розв’язання
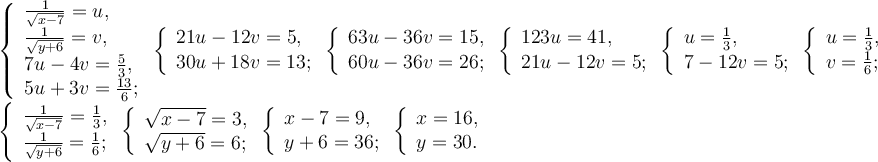
Відповідь: (16; 30).
Використання теореми Вієта
Наприклад: Розв’яжіть систему
![]()
Розв’язання
х і у – корені рівняння ![]() .
.
Звідси а=2, а=3. Отже, розв’язками системи є пари (2;3), (3;2).
Відповідь: (2;3), (3;2).
Симетричні системи
Наприклад: Розв’яжіть систему
![]()
Розв’язання
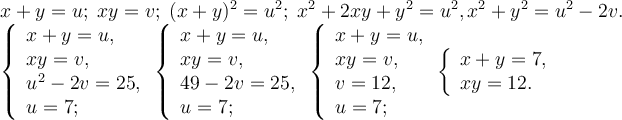
Звідси (3;4), (4;3).
Відповідь: (3;4), (4;3).