Підготовка до ЗНО з математики. Геометрія.

1. Декартові координати

Декартова система координат на площині задається двома взаємно перпендикулярними осями (вісь ОХ – вісь абсцис, вісь ОУ – вісь ординат), які мають спільний початок О (початок координат) і однаковий масштаб осей.

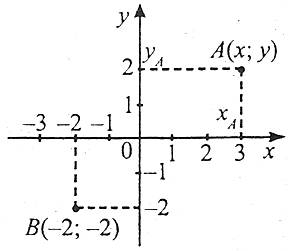
Кожній точці площини за певним правилом ставиться у відповідність пара чисел – абсциса та ордината (х;у), ці числа називаються декартовими координатами точки.

2. Визначення декартових координат на площині

Правило визначення декартових координат на площині

Через точку А проводимо пряму, паралельну осі ординат (ОУ), до перетину її з віссю абсцис у точці х_А. Число х, абсолютна величина якого дорівнює відстані від точки О до точки х_А, називається абсцисою точки А.

Через точку А проводимо пряму, паралельну осі ординат (ОХ), до перетину її з віссю абсцис у точці у_А. Число у, абсолютна величина якого дорівнює відстані від точки О до точки у_А, називається ординатою точки А.

Декартові координати точки записують у дужках поруч із буквеним позначенням точки А(х;у), причому першою в дужках стоїть абсциса, другою – ордината.

Початок координат О розподіляє кожну вісь на дві піввісі, одна з яких вважається додатною, а інша – від’ємною.

Наприклад: точка А має координати 3 і 2, точка В – координати -2 і -2.

Будь-якій парі чисел х і у відповідає лише одна точка площини А(х;у).

3. Відстань між двома точками

Відстань між двома точками дорівнює квадратному кореню із суми квадратів різниць однойменних координат.

Відстань між двома точками на площині

де d – відстань між точкою А1 із координатами (х1;у1) і точкою А2 із координатами (х2;у2).

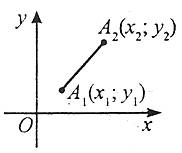
4. Координати середини відрізка

Координати середини відрізка дорівнюють півсумі відповідних координат його кінців.

Координати середини відрізка на площині

Координати (х_с;у_с) точки С, що є серединою відрізка, визначаються за формулами

,

де (х₁;у₁) і (х₂;у₂) – координати точок А₁ і А₂, що є кінцями відрізка.

 

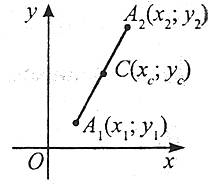
5. Рівняння кола

Рівнянням фігури в декартових координатах на площині (у просторі) називається рівняння із двома невідомими х, у (із трьома невідомими х, у, z), які задовольняють координати будь-якої точки фігури, і тільки вони.

Рівняння кола

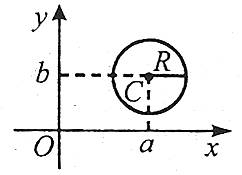
Якщо на площині задано деяку точку з координатами С(а,b), що є центром кола, а також радіус R, то рівняння кола має вигляд

.

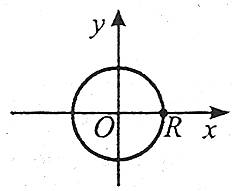
Якщо центром кола є початок координат, то маємо

.

6. Рівняння прямої

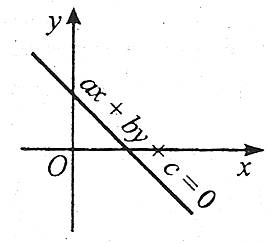
   Загальне повне рівняння будь-якої прямої у декартових координатах х, у має вигляд

ах+bу+с=0,

де а, b, с – деякі числа.

Якщо хоч один коефіцієнт у рівнянні прямої дорівнює нулю, рівняння називається неповним.

Розташування прямої відносно осей координат залежить від коефіцієнтів а, b, с.

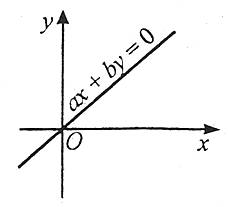
1. Якщо а≠0, b≠0, с=0, то пряма ах+bу=0 проходить через початок координат.

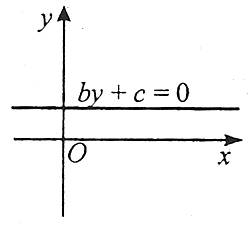
2. Якщо а=0, b≠0, с≠0, то пряма bу+с=0 проходить паралельно осі ОХ.

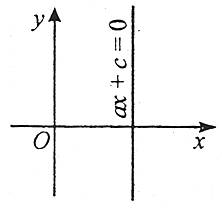
3. Якщо а≠0, b=0, с≠0, то пряма ах+с=0 проходить паралельно осі ОУ.

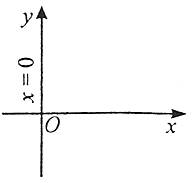
4. Якщо а≠0, b=0, с=0, одержимо х=0, що є рівнянням осі ОУ.

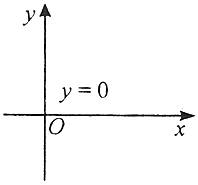
5. Якщо а=0, b≠0, с=0, одержимо у=0, що є рівнянням осі ОХ.

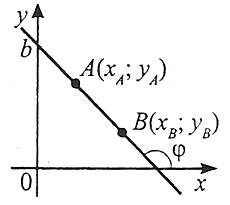
Якщо b≠0, то рівняння прямої можна записати у вигляді , де k – кутовий коефіцієнт прямої,  або .

7. Умови паралельності двох прямих

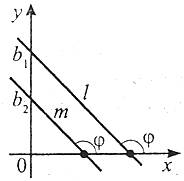
Якщо прямі l та m задано відповідно рівняннями  і , то вони паралельні тоді і тільки тоді, коли .

Якщо , то прямі l та m збігаються.

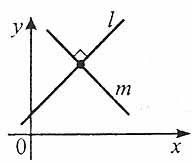
8. Умови перпендикулярності двох прямих

Якщо прямі l та m задано відповідно рівняннями  і , то вони перпендикулярні тоді і тільки тоді, коли .

9. Перетворення фігур на площині

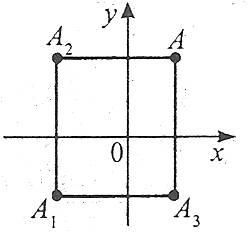
Симетрія

Симетрія відносно	А(1;1)	А(х;у)
точки О	А1(-1;-1)	А1(-х;-у)
осі х	А3(1;-1)	А3(х;-у)
осі у	А2(-1;1)	А2(-х;у)

Паралельне перенесення

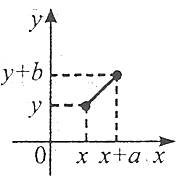
Гомотетія відносно точки О

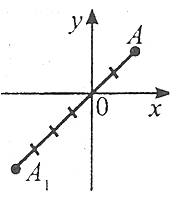
Поворот навколо точки О