КВАДРАТИЧНА ФУНКЦІЯ. КВАДРАТНІ РІВНЯННЯ, НЕРІВНОСТІ ТА ЇХ СИСТЕМИ
6. Розв’язування нерівностей другого степеня з однією змінною
Нерівність, лівою частиною якої є квадратний тричлен  , де а≠0; b, с – дані числа, а правою – нуль, називають квадратною.
, де а≠0; b, с – дані числа, а правою – нуль, називають квадратною.
Наприклад: нерівності  є квадратними, або нерівностями другого степеня з однією змінною.
є квадратними, або нерівностями другого степеня з однією змінною.
Розв’язати нерівність другого степеня з однією змінною означає знайти всі її розв’язки або довести, що їх немає. Під час розв’язування квадратної нерівності знаходять проміжки, у яких відповідна квадратична функція набуває додатних, від’ємних, недодатних, невід’ємних значень.
Приклад 1. Розв’яжіть нерівність  .
.
Розв’язання
Графік функції  - парабола, вітки якої напрямлені вгору. Знайдемо нулі функції, для цього розв’яжемо рівняння . Корені цього рівняння дорівнюють
- парабола, вітки якої напрямлені вгору. Знайдемо нулі функції, для цього розв’яжемо рівняння . Корені цього рівняння дорівнюють
Отже, парабола перетинає вісь х у двох точка, абсциси яких дорівнюють -8 і 6.
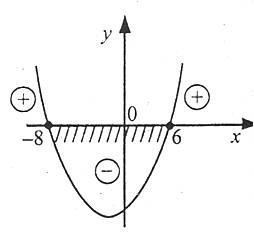
На рис. видно, що функція набуває від’ємних значень, коли х належить проміжку (-8;6). Значить, розв’язком нерівності  є числовий проміжок (-8;6).
є числовий проміжок (-8;6).
Відповідь: (-8;6).
На рис. видно, що:
1. розв’язками нерівності  є всі числа проміжка [-8;6];
є всі числа проміжка [-8;6];
2. розв’язками нерівності  є всі числа проміжків (-∞;-8) або (6;+∞), тобто об’єднання проміжків
є всі числа проміжків (-∞;-8) або (6;+∞), тобто об’єднання проміжків  ;
;
3. розв’язками нерівності  є об’єднання проміжків
є об’єднання проміжків ![( - \infty ; - 8] \cup [6; + \infty ) ( - \infty ; - 8] \cup [6; + \infty )](http://zno.academia.in.ua/filter/tex/pix.php/e9cbd7b3d6109f20db3760d3599edf53.gif) .
.
Приклад 2. Розв’яжіть нерівність  .
.
Розв’язання
Розглянемо функцію  . Її графік – парабола, вітки якої напрямлені догори.
. Її графік – парабола, вітки якої напрямлені догори.
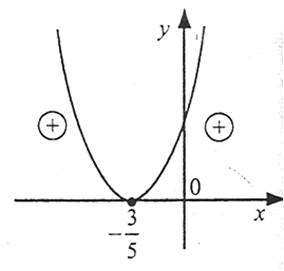
Розв’яжемо рівняння  , звідси х=-0,6. Рівняння має єдиний корінь. Отже, парабола дотикається осі ОХ. На рис. видно, що функція набуває додатних значень при будь-яких х, крім -0,6.
, звідси х=-0,6. Рівняння має єдиний корінь. Отже, парабола дотикається осі ОХ. На рис. видно, що функція набуває додатних значень при будь-яких х, крім -0,6.
Із рис. випливає також, що:
1. розв’язком нерівності  є всі дійсні числа;
є всі дійсні числа;
2. нерівність  має один розв’язок: х=-0,6;
має один розв’язок: х=-0,6;
3. нерівність  розв’язків не має.
розв’язків не має.
Приклад 3. Розв’яжіть нерівність  .
.
Розв’язання
Графік функції  - парабола, вітки якої напрямлені вниз. Рівняння дійсних коренів не має, тому парабола не перетинає вісь ОХ. Отже, вона розташована нижче осі ОХ.
- парабола, вітки якої напрямлені вниз. Рівняння дійсних коренів не має, тому парабола не перетинає вісь ОХ. Отже, вона розташована нижче осі ОХ.
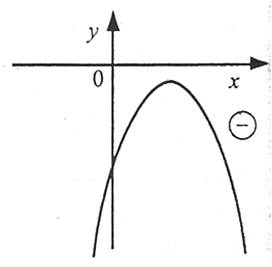
Це означає, що значення квадратичної функції при всіх х – від’ємні, тобто нерівність  виконується при всіх дійсних числах (-∞;+∞).
виконується при всіх дійсних числах (-∞;+∞).
Відповідь: (-∞;+∞).
Із рис. видно також, що:
1. розв’язками нерівності  є множина всіх дійсних чисел R;
є множина всіх дійсних чисел R;
Із розглянутих прикладів можна зробити висновок, що для розв’язування квадратних нерівностей за допомогою графіків треба:
1. визначити напрям віток параболи за значенням першого коефіцієнта квадратичної функції  (якщо а>0, то вітки параболи напрямлені догори, якщо а<0, то вниз);
(якщо а>0, то вітки параболи напрямлені догори, якщо а<0, то вниз);
2. знайти дійсні корені квадратного рівняння  або встановити, що їх немає;
або встановити, що їх немає;
3. схематично побудувати графік квадратичної функції, використовуючи точки перетину (точки дотику) із віссю ОХ, якщо вони є;
4. за графіком визначити проміжки, на яких функція набуває значень, при яких виконується задана нерівність.
Квадратні нерівності можна розв’язувати методом інтервалів.



