Підготовка до ЗНО з математики. Алгебра.

     Використовується для розв’язування нерівностей f(x)>0 (f(x)<0, f(x)≥0, f(x)≤0). Метод ґрунтується на тому, що неперервна на проміжку функція може змінювати знак тільки в тих точках, де її значення дорівнює нулю (але може й не змінювати).

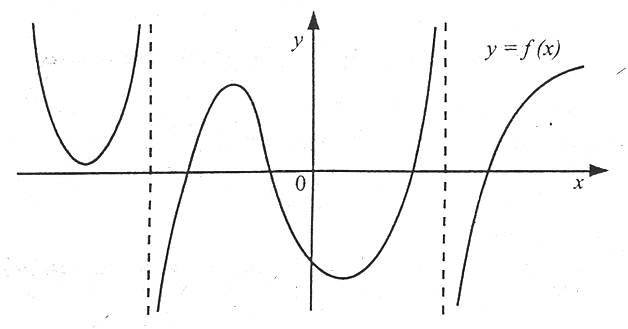
     Щоб розв’язати нерівність методом інтервалів, потрібно:

1. знайти область визначення функції y=f(x);

2. знайти значення х, при яких функція дорівнює нулю (знайти всі нулі функції): f(x)=0;

3. розбити область визначення на проміжки, у яких кожен із кінців є коренем рівняння f(x)=0 або кінцевою точкою проміжку визначення функції y=f(x);

4. визначити знак f(x) на кожному з утворених проміжків;

5. об’єднати проміжки, на яких функція f(x) задовольняє нерівність, у множину розв’язків.

    Приклад 5. Розв’яжіть нерівність $\frac{{{x^2} - 2x - 3}}{{{x^2} + 3x - 4}} \ge 0$.

Розв’язання

     Розкладемо чисельник і знаменник дробу на множники й одержимо

$\frac{{(x - 3)(x + 1)}}{{(x - 1)(x + 4)}} \ge 0$.

     Позначимо на силовій прямій точки 3; -1; 1; -4, у яких чисельник або знаменник дробу перетворюється на нуль. Ці точки поділяють числову пряму на п’ять проміжків. При х>3 усі множники чисельника і знаменника дробу додатні, то дріб є додатним.

     При переході від одного проміжку до іншого дріб змінює знак, тому можна розставити знаки. Значення х=-1, х=3 задовольняють дану нерівність, а при х=1, х=-4 дріб не має змісту. Таким чином дана нерівність має розв’язок $( - \infty ; - 4) \cup [ - 1;1) \cup [3; + \infty )$.

     Відповідь: $( - \infty ; - 4) \cup [ - 1;1) \cup [3; + \infty )$.