СИНУС, КОСИНУС, ТАНГЕНС І КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТУ
2. Означення синуса, косинуса, тангенса і котангенса
Розглянемо на координатній площині коло радіуса 1 із центром у початку координат, яке називають одиничним.
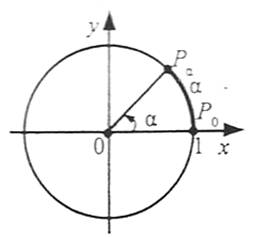
Позначимо точку P0 – правий кінець горизонтального діаметра. Поставимо у відповідність кожному дійсному числу α точку кола за такими правилами:
1) якщо α>0, то, рухаючись по колу з точки Р0 у напрямі проти годинникової стрілки (додатний напрям обходу кола), опишемо по колу шлях довжиною α. Кінцева точка цього шляху і буде шуканою точкою Рα;
2) якщо α<0, то, рухаючись із точки Р0 у напрямі за годинниковою стрілкою, опишемо по колу шлях довжиною |α|. Кінець цього шляху і буде шуканою точкою Рα;
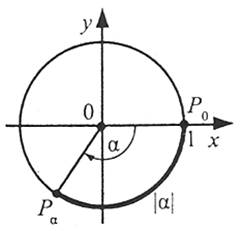
3) якщо α=0, то поставимо у відповідність точку Р0.
Таким чином, кожному дійсному числу можна поставити у відповідність Рα одиничного кола.
Якщо α=α0+2πk, де k – ціле число, то при повороті на кут α одержуємо ту саму точку, що й при повороті на кут α0.
Якщо точка Р відповідає числу α, то вона відповідає і всім числам виду α+2πk, де 2π – довжина кола (бо радіус дорівнює 1), а k – ціле число, що показує кількість повних обходів кола в тому чи іншому напрямі.
Синусом числа α називають ординату точки Рα, утвореної поворотом точки Р0(1;0) навколо початку координат на кут α радіан (позначають sin α).
Синус визначено для будь-якого числа α.
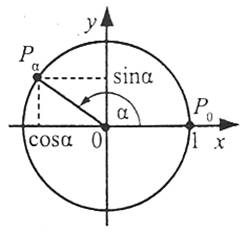
Косинусом числа α називають абсцису точки Рα, утвореної поворотом точки Р0(1;0) навколо початку координат на кут α радіан (cos α).
Косинус визначено для будь-якого числа α.
Тангенсом числа α називають відношення синуса числа α до його косинуса
Тангенс визначено для всіх α, крім тих значень, для яких cos α=0, тобто для  .
.
Для розв’язування деяких задач корисно мати уявлення про лінію тангенсів.
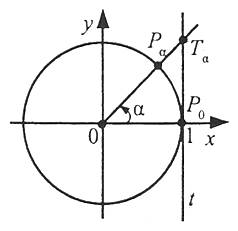
Проведемо дотичну t до одиничного кола в точці Р0. Нехай α – довільне число, для якого cos α≠0, тоді точка Рα (cos α; sin α) не лежить на осі ординат і пряма ОРα перетинає дотичну t у деякій точці Тα з абсцисою 1. Знайдемо ординату точки Тα з ΔОР0Тα:
Таким чином, ордината точки перетину прямих ОРα і t дорівнює тангенсу числа α. Тому пряму t називають віссю тангенсів.
Котангенс числа α – це відношення косинуса числа α до його синуса
Котангенс визначено для всіх α, крім таких значень, для яких sin α=0, тобто для  .
.
Уведемо поняття лінії котангенсів.
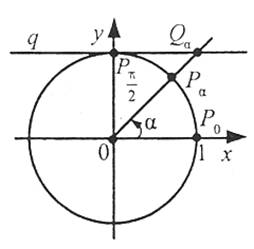
Проведемо дотичну q до одиничного кола в точці . Для довільного числа α, якщо sin α≠0, відповідна точка Рα(cos α; sin α) не лежить на осі ОХ, тому пряма ОРα перетинає пряму q в деякій точці Qα з ординатою 1. Із трикутника  маємо:
маємо:  , звідси х=ctg α. Таким чином, абсциса точки перетину прямих ОРα і q дорівнює котангенсу числа α, тому пряму q називають віссю котангенсів.
, звідси х=ctg α. Таким чином, абсциса точки перетину прямих ОРα і q дорівнює котангенсу числа α, тому пряму q називають віссю котангенсів.
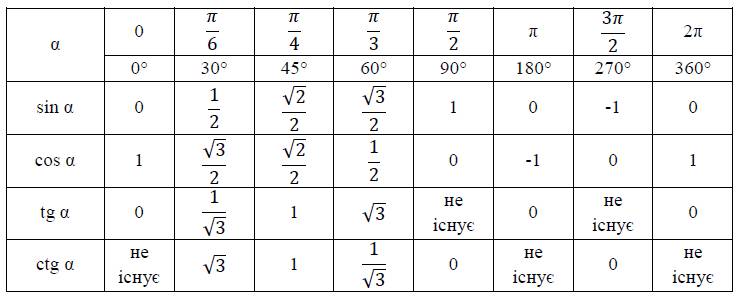
Нижче наведено таблицю значень синусів, косинусів, тангенсів і котангенсів деяких кутів.