Похідна функції, її геометричний та механічний зміст
Фізичний зміст похідної
Нехай матеріальна точка М рухається прямолінійно за законом s=f(t).
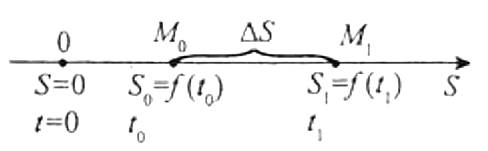
У момент t0 вона зайняла положення М0 і пройшла шлях s0=f(t0). Знайдемо швидкість точки в момент t0.
Припустимо, що за довільно вибраний проміжок часу Δt, починаючи з моменту t0, точка перемістилася на відстань Δs і зайняла положення М1.
Тоді t1=t0+Δt, s1=f(t1)=s0+Δs.
За проміжок часу Δt матеріальна точка проходить шлях
ΔS=f(t1)-f(t0)=f(t0+Δt)-f(t0).
Середня швидкість (vсер.) руху на проміжку М0М1 дорівнює
Ця величина дає лише приблизне уявлення про швидкість руху матеріальної точки на розглянутому проміжку. Вона буде точнішою, якщо проміжок Δt зменшуватиметься.
Таким чином, можна вважати, якщо Δt наближається до нуля, то середня швидкість  буде наближатися до швидкості в момент t0.
буде наближатися до швидкості в момент t0.
Миттєвою швидкістю точки, яка рухається прямолінійно, у момент t0 називають границею середньої швидкості за умови, що Δt наближається до нуля:
Числа Δt, Δs називають відповідно приростом часу і приростом шляху.
Отже, миттєвою швидкістю точки, яка рухається прямолінійно, є границя відношення приросту шляху Δs до відповідного приросту часу Δt, коли приріст часу наближається до нуля.
Порівнюючи одержані результати з означенням похідної, можна зробити висновок: якщо матеріальна точка рухається прямолінійно і її координата змінюється за законом s=s(t), то швидкість її руху v(t) у момент t дорівнює похідній  :
:


