ЛІНІЙНА ФУНКЦІЯ. ЛІНІЙНІ РІВНЯННЯ, НЕРІВНОСТІ ТА ЇХ СИСТЕМИ
Лінійна функція. Лінійні рівняння, нерівності та їх системи
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | ЛІНІЙНА ФУНКЦІЯ. ЛІНІЙНІ РІВНЯННЯ, НЕРІВНОСТІ ТА ЇХ СИСТЕМИ |
| Надруковано: | Гість |
| Дата: | Tuesday 1 July 2025 8:42 AM |
1. Лінійна функція
Лінійною називають функцію виду  , де k і b – дійсні числа.
, де k і b – дійсні числа.
Основні властивості лінійних функцій подано в таблиці.
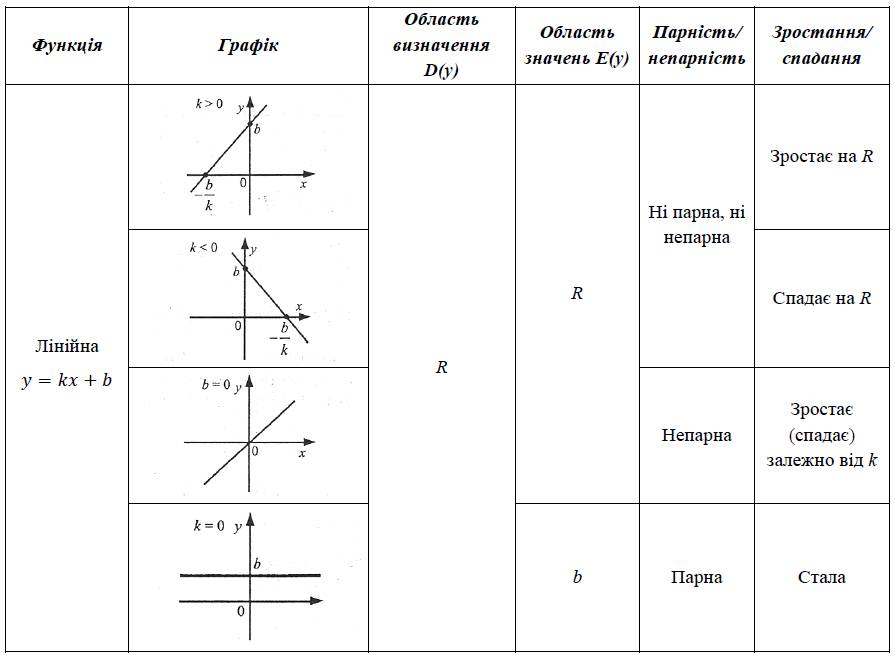
2. Лінійне рівняння з однією змінною
Лінійним рівнянням з однією змінною називають рівняння виду  , де х – змінна, а і b – числа.
, де х – змінна, а і b – числа.
Якщо а≠0, то рівняння  має єдиний корінь
має єдиний корінь  .
.
Наприклад: рівняння 5х=6 має корінь х=1,2.
Якщо а=0, b≠0, то рівняння  не має коренів.
не має коренів.
Наприклад: рівняння 0х=5 не має коренів.
Якщо а=0, b=0, то коренем рівняння  є будь-яке число.
є будь-яке число.
Деякі рівняння зводяться до розв’язування лінійних рівнянь. Розглянемо приклади.
Приклад 1. Розв’яжіть рівняння  .
.
Розв’язання
Щоб позбутися знаменників дробів, помножимо кожний член рівняння на найменший спільний знаменник дробів, тобто на 20, і отримаємо:
40-5(3х-4)+4(х+18)=0.
Розкриємо дужки:
40-15х+20+4х+72=0.
Залишимо члени зі змінними в лівій частині рівняння, а члени без змінних перенесемо в праву частину (змінивши знаки членів на протилежні):
-15х+4х=-40-20-72.
Зведемо подібні доданки:
-11х=-132, звідси х=-132:(-11), х=12.
Відповідь: 12.
Приклад 2. Розв’яжіть рівняння (2х-6)(х+2)=0.
Розв’язання
Якщо добуток кількох множників дорівнює нулю, то хоча б один із множників дорівнює нулю. Скористаємося цим фактом при розв’язуванні даного рівняння.
Ліва частина рівняння – добуток невідомих множників 2х-6 і х+2, а права частина – нуль. Щоб розв’язати це рівняння, досить прирівняти до нуля множники 2х-6 і х+2 та розв’язати отримані рівняння. Отже, 2х-6=0 або х+2=0, тоді 2х-6=0, 2х=6, х=6:2, х=3 або х+2=0, х=-2.
Відповідь: 3, -2.
Приклад 3. Розв’яжіть рівняння  .
.
Розв’язання
Згадаймо значення модуля:
Із точки зору геометрії |х| означає відстань від точки х, зображеної на координатній прямій, до початку координат (точки 0).
1-й спосіб.
Якщо 2х+3<0, то за означенням модуля –(2х+3)=1, тоді 2х+3=-1, 2х=-3-1, 2х=-4, х=-2.
Якщо 2х+3≥0, то за означенням модуля 2х+3=1, тоді 2х+3=1, 2х=-3+1, 2х=-2, х=-1.
Відповідь: -1; -2.
2-й спосіб.
Ураховуючи геометричний зміст модуля, рівність |2х+3|=1 означає, що відстань від точки 2х+3 до початку координат дорівнює числу 1, тобто
![]()
1) 2х+3=-1, 2х=-3-1, 2х=-4, х=-2;
2) 2х+3=1, 2х=-3+1, 2х=-2, х=-1.
Відповідь: -1; -2.
3. Лінійні нерівності з однією змінною
Нерівності виду  - деякі числа, а х – змінна, називають лінійними нерівностями з однією змінною.
- деякі числа, а х – змінна, називають лінійними нерівностями з однією змінною.
Розглянемо нерівність ax>b.
1. Якщо а>0, то  . Наприклад: 3х>6, х>2.
. Наприклад: 3х>6, х>2.
2. Якщо а<0, то  . Наприклад: -2х>4, х<-2.
. Наприклад: -2х>4, х<-2.
3. Якщо а=0, b<0, то розв’язком нерівності є множина всіх дійсних чисел R. Наприклад: 0х>-5,  .
.
4. Якщо а=0, b>0, то нерівність розв’язків не має. Наприклад: 0х>5 не має розв’язків.
Розглянемо нерівність ax<b.
1. Якщо а>0, то  . Наприклад:
. Наприклад:  .
.
2. Якщо а<0, то  . Наприклад:
. Наприклад:  .
.
3. Якщо а=0, b<0, то нерівність розв’язків не має. Наприклад: 0х<-5 розв’язків не має.
4. Якщо а=0, b>0, то розв’язком нерівності є множина всіх дійсних чисел R. Наприклад: нерівність 0х<5,  .
.
У рівнянні, крім невідомого, яке потрібно знайти, можуть бути введені й інші букви.
Наприклад: ах=3-а, (n+2)x=2+(n+2).
Розгляньмо рівняння ах=3-а, яке залежно від змінної а матиме вигляд:
2х=3-2, якщо а=2;
0х=3-0, якщо а=0;
3х=3-3, якщо а=3 і т.д.
Змінну, яку потрібно знайти, будемо називати невідомою, іншу змінну – параметром.
Розв’язати рівняння з параметром означає, що для кожного значення параметра треба встановити, чи має рівняння розв’язки, і якщо має, то знайти ці розв’язки, що, як правило, залежать від параметра. Розглянемо приклади.
Приклад 4. Розв’яжіть рівняння х+5=а+6 відносно х.
Розв’язання
Перетворивши рівняння, отримаємо: х=а+1.
Рівняння має єдиний розв’язок незалежно від значення параметра.
Отже, х=а+1.
Відповідь: а+1.
Приклад 5. Розв’яжіть рівняння (а-1)х=3 відносно х.
Розв’язання
Якщо а-1≠0, тобто а≠1, то рівняння має єдиний корінь  .
.
Якщо а-1=0, тобто а=1, то рівняння набуває вигляду 0х=3 і не має коренів.
Відповідь: при а≠1 дане рівняння має єдиний корінь  , а при а=1 – коренів не має.
, а при а=1 – коренів не має.
Приклад 6. Розв’яжіть нерівність  .
.
Розв’язання
Помножимо обидві частини нерівності на 4:
4х-2(х+3)≥2х-1.
Розкриємо дужки в лівій частині: 4х-2х-6≥2х-1. Перенесемо члени нерівності зі змінними в ліву частину нерівності, а члени без змінних – у праву частину (змінивши знаки членів, які переносимо, на протилежні): 4х-2х-2х≥-1+6, звідси маємо 0х≥5. Отже, дана нерівність розв’язків не має.
Відповідь: нерівність розв’язків немає.
4. Системи лінійних рівнянь з двома змінними
Системи рівнянь розв’язують кількома способами: графічним, підстановки, додавання. Розглянемо приклади.
Приклад 7. Розв’яжіть систему рівнянь графічним способом
Розв’язання
Побудуємо графіки рівнянь х+у=5 або у=-х+5 (пряма, яка проходить через точки (0;5) і (5;0)) та х-у=1 або у=х-1 (пряма, яка проходить через точки (0;-1) та (1;0)).
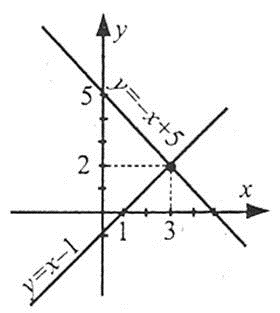
Ці графіки перетинаються в точці (3;2).
Отже, розв’язком системи є пара (3;2).
Відповідь: (3;2).
Щоб розв’язати систему рівнянь графічним способом, треба:
1. виконати рівносильні перетворення системи так, щоб було зручно побудувати графіки рівнянь системи;
2. побудувати графіки;
3. знайти координати точок (точки) перетину побудованих ліній. Ці координати і є розв’язками (розв’язком) системи рівнянь.
Зауваження. Графічний спосіб розв’язування систем рівнянь не є універсальним, оскільки не завжди розв’язком системи є пара цілих чисел. Іноді важко точно встановити координати точки перетину побудованих графіків функцій, можливо лише вказати наближенні значення. Тому, як правило, використовують алгебрагічні способи розв’язування систем рівнянь: спосіб підстановки, додавання.
Приклад 8. Розв’яжіть систему рівнянь способом підстановки
Розв’язання
Із першого рівняння системи виразимо у через х: у=6-2х. одержаний вираз підставимо в друге рівняння системи:
4х-3(6-2х)=2, звідси 4х-18+6х=2; 10х=20; х=2.
Одержане значення х підставляємо у вираз у=6-2х;
у=6-2·2.
Отже, пара (2;2) – розв’язок даної системи.
Відповідь: (2;2).
Способом підстановки систему двох рівнянь із двома змінними розв’язують за таким порядком:
1. з одного рівняння системи виражаємо одну зі змінних через другу змінну і відомі величини;
2. знайдене значення підставляємо в друге рівняння системи, одержуємо рівняння відносно другої змінної;
3. розв’язуємо одержане рівняння і знаходимо значення цієї змінної;
4. підставляючи знайдене значення у вираз для першої змінної, одержуємо відповідне її значення;
5. записуємо відповідь.
Зауваження. Спосіб підстановки, як правило, використовують, якщо коефіцієнт при одній зі змінних в одному з рівнянь системи дорівнює 1.
Приклад 9. Розв’яжіть систему рівнянь способом додавання
Розв’язання
Помножимо почленно перше рівняння системи на 3, а друге – на 2 (це дає змогу при додаванні рівнянь позбавитися від змінної у):
Додавши почленно рівняння, одержуємо 19х=19, звідси х=1 (значення у знайдемо з першого рівняння системи: 3·1+2у=5, 2у=2, у=1, отже, (1;1) – розв’язок системи).
Значення у можна знайти, якщо помножимо почленно перше рівняння на -5, а друге – на 3:
Додавши почленно рівняння, одержуємо:
-19у=-19, у=1.
Отже, пара (1;1) є розв’язком даної системи.
Відповідь: (1;1).
Розв’язування системи двох лінійних рівнянь із двома змінними способом алгебрагічного додавання виконують за таким порядком:
1) урівнюємо коефіцієнти при одній зі змінних шляхом по членного множення обох рівнянь на множники, підібрані відповідним чином;
2) додаючи (або віднімаючи) почленно рівняння системи, виключаємо одну зі змінних;
3) розв’язуємо одержане рівняння з однією змінною;
4) значення другої змінної можна знайти таким же способом (або підстановкою знайденого значення змінної в будь-яке із заданих рівнянь системи);
5) записуємо відповідь.
Зауваження. Спосіб додавання, як правило, використовують, якщо коефіцієнти при одній зі змінних у рівнянні системи – протилежні числа.
5. Системи лінійних нерівностей з однією змінною
Приклад 10. Розв’яжіть систему нерівностей
Розв’язання
Маємо
Зображаємо на числовій прямій множини розв’язків кожної з нерівностей
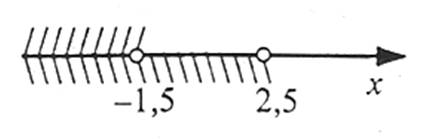
Обидві нерівності справедливі при х≤-1,5. Відповідь можна записати у вигляді нерівності х≤-1,5 або у вигляді числового проміжку (-∞;-1,5].
Відповідь: (-∞;-1,5].
Приклад 11. Розв’яжіть систему нерівностей
Розв’язання
Маємо
Використовуючи числову пряму, знайдемо спільні розв’язки нерівностей  і
і  .
.
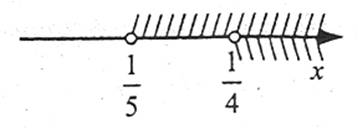
Бачимо, що множина розв’язків системи складається із чисел, які задовольняють умові  , тобто є числовим проміжком
, тобто є числовим проміжком  .
.
Приклад 12. Розв’яжіть систему нерівностей
Розв’язання
Маємо
Використовуючи числову пряму, знаходимо, що спільних розв’язків нерівності х>0 і х<-0,2 не мають. Отже, дана система розв’язків не має.
![]()
Відповідь: розв’язків не має.
Приклад 13. Розв’яжіть систему нерівностей
Розв’язання
Маємо
Розв’язком першої і другої нерівностей є числова пряма (-∞;+∞). Отже, розв’язком даної системи є будь-яке число х.
Відповідь: (-∞;+∞).
Приклад 14. Розв’яжіть нерівність (х-3)(2-х)≥0.
Розв’язання
Добуток двох множників невід’ємний, коли обидва множники або невід’ємні, або недодатні. Тому розв’язування даної нерівності зводиться до розв’язування двох систем нерівностей:
Тоді маємо:
Оскільки перша система не має розв’язків, а розв’язком другої системи є проміжок [2;3], то дана система має множину розв’язків – [2;3].
Відповідь: [2;3].
Приклад 15. Розв’яжіть нерівність  .
.
Розв’язання
Дріб від’ємний, коли значення чисельника і знаменника мають протилежні знаки, тому розв’язування даної нерівності зводиться до розв’язування двох систем нерівностей:
Тоді маємо:
Оскільки друга система не має розв’язків, а розв’язком першої системи є проміжок (-1;1), то дана система має множину розв’язків – (-1;1).
Відповідь: (-1;1).





















