КВАДРАТИЧНА ФУНКЦІЯ. КВАДРАТНІ РІВНЯННЯ, НЕРІВНОСТІ ТА ЇХ СИСТЕМИ
Квадратична функція. Квадратні рівняння, нерівності та їх системи
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | КВАДРАТИЧНА ФУНКЦІЯ. КВАДРАТНІ РІВНЯННЯ, НЕРІВНОСТІ ТА ЇХ СИСТЕМИ |
| Надруковано: | Гість |
| Дата: | Tuesday 1 July 2025 2:40 AM |
1. Квадратична функція
Квадратичною називають функцію виду  , де а, b, с – дійсні числа, причому а≠0.
, де а, b, с – дійсні числа, причому а≠0.
Основні властивості квадратичних функцій подано в таблиці.
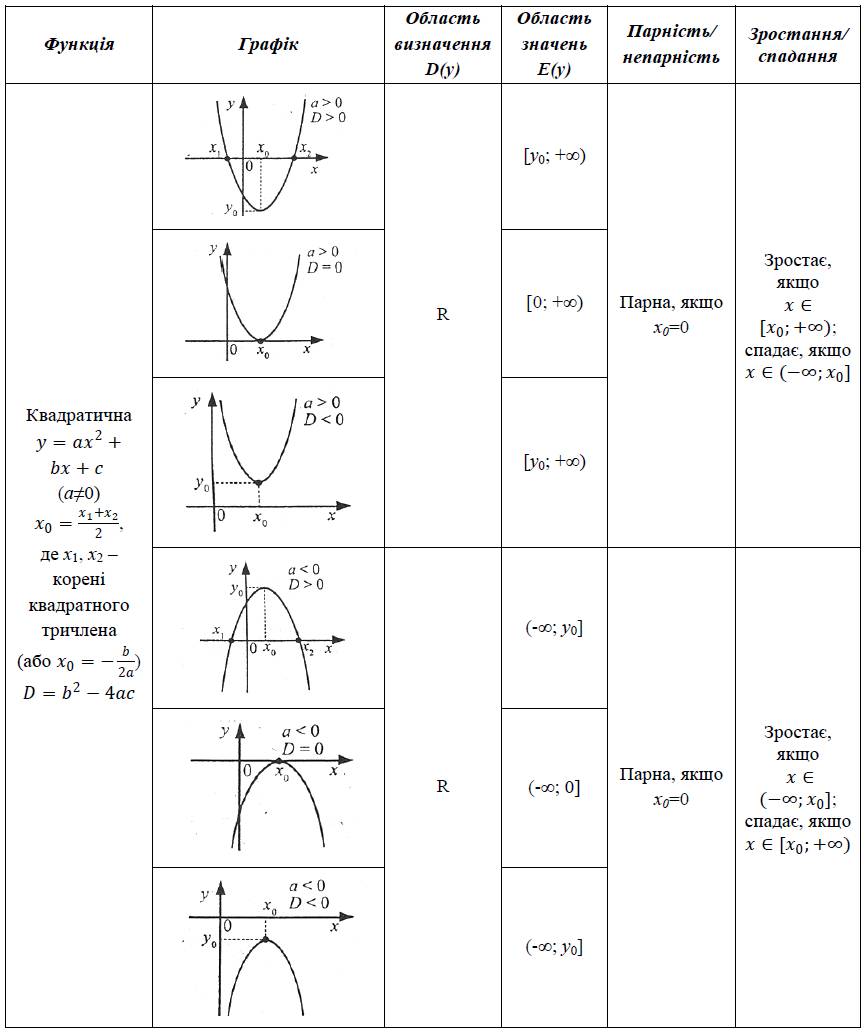
2. Квадратне рівняння
Квадратним називають рівняння виду  , де х – змінна; а, b, с – числа, причому а≠0. Число а називають першим (старшим) коефіцієнтом, b – другим коефіцієнтом, с – вільним членом.
, де х – змінна; а, b, с – числа, причому а≠0. Число а називають першим (старшим) коефіцієнтом, b – другим коефіцієнтом, с – вільним членом.
Квадратне рівняння, у якого перший коефіцієнт дорівнює числу 1, називають зведеним квадратним рівнянням.
Квадратне рівняння, у якого хоча б один з коефіцієнтів – b або с – дорівнює нулю, називають неповним квадратним рівнянням.
Неповне квадратне рівняння виду 
Рівняння виду завжди має два корені: 0 і  . Такі рівняння, як правило розв’язують розкладанням його лівої частини на множники.
. Такі рівняння, як правило розв’язують розкладанням його лівої частини на множники.
Неповне квадратне рівняння виду 
Якщо  , то рівняння виду
, то рівняння виду  має два корені:
має два корені:  та
та  .
.
3. Формула коренів квадратного рівняння
Вираз  називають дискримінантом квадратного рівняння
називають дискримінантом квадратного рівняння  .
.
Якщо D>0, то квадратне рівняння має два корені; якщо D=0, то один корінь; якщо D<0, то квадратне рівняння коренів не має.
Корені квадратного рівняння  при D≥0 знаходять за формулою
при D≥0 знаходять за формулою
Для квадратного рівняння виду  формула коренів має вигляд
формула коренів має вигляд
Для зведеного квадратного рівняння виду  формула коренів має вигляд
формула коренів має вигляд
4. Квадратний тричлен
Квадратним тричленом називають многочлен виду  , де х – змінна; а, b, с – деякі дійсні числа, причому а≠0.
, де х – змінна; а, b, с – деякі дійсні числа, причому а≠0.
Наприклад: вирази  – квадратні тричлени.
– квадратні тричлени.
Коренем квадратного тричлена називають значення змінної, при якому значення цього тричлена дорівнює нулю.
Наприклад: коренем тричлена  є число -1, бо при х=-1 маємо
є число -1, бо при х=-1 маємо  .
.
Квадратний тричлен має не більше двох коренів:
- якщо D<0, то квадратний тричлен не має коренів;
- якщо D=0, то квадратний тричлен має два рівних корені
 ;
; - якщо D>0, то квадратний тричлен має два різних корені
 .
.
Число D називають дискримінантом квадратного тричлена.
Теорема Вієта
Якщо  - корені квадратного тричлена
- корені квадратного тричлена  , то виконуються рівності
, то виконуються рівності
5. Розкладання квадратного тричлена на множники
Якщо  , то виконується рівність
, то виконується рівність
де  - корені квадратного тричлена.
- корені квадратного тричлена.
Доведення
Згідно з теоремою Вієта маємо  .
.
Якщо  , то виконується рівність
, то виконується рівність
Якщо  , то квадратний тричлен не можна розкласти на лінійні множники у множині дійсних чисел.
, то квадратний тричлен не можна розкласти на лінійні множники у множині дійсних чисел.
6. Розв’язування нерівностей другого степеня з однією змінною
Нерівність, лівою частиною якої є квадратний тричлен  , де а≠0; b, с – дані числа, а правою – нуль, називають квадратною.
, де а≠0; b, с – дані числа, а правою – нуль, називають квадратною.
Наприклад: нерівності  є квадратними, або нерівностями другого степеня з однією змінною.
є квадратними, або нерівностями другого степеня з однією змінною.
Розв’язати нерівність другого степеня з однією змінною означає знайти всі її розв’язки або довести, що їх немає. Під час розв’язування квадратної нерівності знаходять проміжки, у яких відповідна квадратична функція набуває додатних, від’ємних, недодатних, невід’ємних значень.
Приклад 1. Розв’яжіть нерівність  .
.
Розв’язання
Графік функції  - парабола, вітки якої напрямлені вгору. Знайдемо нулі функції, для цього розв’яжемо рівняння . Корені цього рівняння дорівнюють
- парабола, вітки якої напрямлені вгору. Знайдемо нулі функції, для цього розв’яжемо рівняння . Корені цього рівняння дорівнюють
Отже, парабола перетинає вісь х у двох точка, абсциси яких дорівнюють -8 і 6.
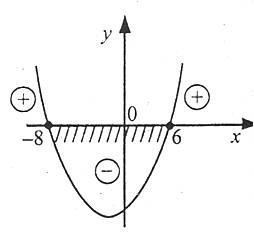
На рис. видно, що функція набуває від’ємних значень, коли х належить проміжку (-8;6). Значить, розв’язком нерівності  є числовий проміжок (-8;6).
є числовий проміжок (-8;6).
Відповідь: (-8;6).
На рис. видно, що:
1. розв’язками нерівності  є всі числа проміжка [-8;6];
є всі числа проміжка [-8;6];
2. розв’язками нерівності  є всі числа проміжків (-∞;-8) або (6;+∞), тобто об’єднання проміжків
є всі числа проміжків (-∞;-8) або (6;+∞), тобто об’єднання проміжків  ;
;
3. розв’язками нерівності  є об’єднання проміжків
є об’єднання проміжків ![( - \infty ; - 8] \cup [6; + \infty ) ( - \infty ; - 8] \cup [6; + \infty )](http://zno.academia.in.ua/filter/tex/pix.php/e9cbd7b3d6109f20db3760d3599edf53.gif) .
.
Приклад 2. Розв’яжіть нерівність  .
.
Розв’язання
Розглянемо функцію  . Її графік – парабола, вітки якої напрямлені догори.
. Її графік – парабола, вітки якої напрямлені догори.
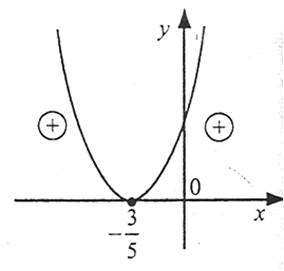
Розв’яжемо рівняння  , звідси х=-0,6. Рівняння має єдиний корінь. Отже, парабола дотикається осі ОХ. На рис. видно, що функція набуває додатних значень при будь-яких х, крім -0,6.
, звідси х=-0,6. Рівняння має єдиний корінь. Отже, парабола дотикається осі ОХ. На рис. видно, що функція набуває додатних значень при будь-яких х, крім -0,6.
Із рис. випливає також, що:
1. розв’язком нерівності  є всі дійсні числа;
є всі дійсні числа;
2. нерівність  має один розв’язок: х=-0,6;
має один розв’язок: х=-0,6;
3. нерівність  розв’язків не має.
розв’язків не має.
Приклад 3. Розв’яжіть нерівність  .
.
Розв’язання
Графік функції  - парабола, вітки якої напрямлені вниз. Рівняння дійсних коренів не має, тому парабола не перетинає вісь ОХ. Отже, вона розташована нижче осі ОХ.
- парабола, вітки якої напрямлені вниз. Рівняння дійсних коренів не має, тому парабола не перетинає вісь ОХ. Отже, вона розташована нижче осі ОХ.
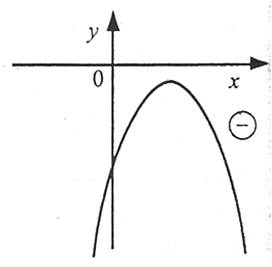
Це означає, що значення квадратичної функції при всіх х – від’ємні, тобто нерівність  виконується при всіх дійсних числах (-∞;+∞).
виконується при всіх дійсних числах (-∞;+∞).
Відповідь: (-∞;+∞).
Із рис. видно також, що:
1. розв’язками нерівності  є множина всіх дійсних чисел R;
є множина всіх дійсних чисел R;
Із розглянутих прикладів можна зробити висновок, що для розв’язування квадратних нерівностей за допомогою графіків треба:
1. визначити напрям віток параболи за значенням першого коефіцієнта квадратичної функції  (якщо а>0, то вітки параболи напрямлені догори, якщо а<0, то вниз);
(якщо а>0, то вітки параболи напрямлені догори, якщо а<0, то вниз);
2. знайти дійсні корені квадратного рівняння  або встановити, що їх немає;
або встановити, що їх немає;
3. схематично побудувати графік квадратичної функції, використовуючи точки перетину (точки дотику) із віссю ОХ, якщо вони є;
4. за графіком визначити проміжки, на яких функція набуває значень, при яких виконується задана нерівність.
Квадратні нерівності можна розв’язувати методом інтервалів.
7. Розв’язування квадратичних нерівностей методом інтервалів
Розглянемо розв’язування квадратичних нерівностей методом інтервалів на прикладі.
Приклад 1. Знайдіть, при яких значення х квадратний тричлен  набуває додатних значень, а при яких – від’ємних.
набуває додатних значень, а при яких – від’ємних.
Розв’язання
Розкладемо квадратний тричлен  на множники
на множники
Тоді х=2 і х=3 поділяють числову пряму на три проміжки: (-∞;2); (2;3); (3;+∞).
![]()
Вираз (х-2)(х-3) є добутком двох множників. Знак кожного з цих множників та їх добутку подамо у вигляді таблиці.
|
|
(-∞;2) |
(2;3) |
(3;+∞) |
|
х-2 |
- |
+ |
+ |
|
х-3 |
- |
- |
+ |
|
(х-2)(х-3) |
+ |
- |
+ |
Рухаючись уздовж числової осі зліва направо, ми бачимо, що на проміжку (-∞;2) тричлен  набуває додатних значень, оскільки в цьому випадку обидва множники х-2 і х-3 є від’ємними.
набуває додатних значень, оскільки в цьому випадку обидва множники х-2 і х-3 є від’ємними.
На проміжку (2;3) цей тричлен набуває від’ємних значень і, отже, при переході через точку х=2 змінює знак. Це відбувається тому, що в добутку (х-2)(х-3) при переході через точку х=2 перший множник х-2 змінює знак, а другий множник х-3 – ні.
При переході через точку х=3 тричлен знову змінює знак, оскільки в добутку (х-2)(х-3) перший множник х-2 не змінює знак, а другий множник х-3 змінює.
Отже, рухаючись уздовж числової прямої, ми спостерігаємо, як змінюється знак добутку (х-2)(х-3).
Таким чином, задачу про знак квадратного тричлена  можна розв’язувати у такий спосіб.
можна розв’язувати у такий спосіб.
Позначити на числовій прямій корені рівняння  , тобто точки х=2, х=3. Вони поділяють числову пряму на три проміжки. На проміжку (-∞;2) значення тричлена
, тобто точки х=2, х=3. Вони поділяють числову пряму на три проміжки. На проміжку (-∞;2) значення тричлена  додатне, тому розставляємо його знаки на останніх проміжках, ураховуючи чергування знаків.
додатне, тому розставляємо його знаки на останніх проміжках, ураховуючи чергування знаків.
![]()
На рис. видно, що  на проміжку
на проміжку  , а на проміжку (2;3) -
, а на проміжку (2;3) -  .
.
Приклад 2. Розв’яжіть нерівність  .
.
Розв’язання
Знайдемо корені квадратного тричлена  :
:
Наносимо на числову пряму точки -1 та  , які поділяють її на три проміжки. Визначаємо знак тричлена
, які поділяють її на три проміжки. Визначаємо знак тричлена  на проміжку (-∞;-1), він на цьому проміжку додатний. Знаходимо знаки тричлена на інших проміжках.
на проміжку (-∞;-1), він на цьому проміжку додатний. Знаходимо знаки тричлена на інших проміжках.
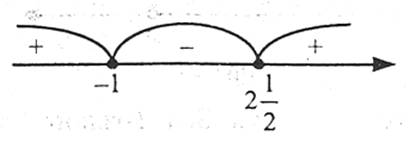



















![( - \infty ; - 1] \cup [2\frac{1}{2}; + \infty ) ( - \infty ; - 1] \cup [2\frac{1}{2}; + \infty )](http://zno.academia.in.ua/filter/tex/pix.php/02a9839c7d5a798a5557717ce6e44ee7.gif)