РАЦІОНАЛЬНІ РІВНЯННЯ, НЕРІВНОСТІ ТА ЇХ СИСТЕМИ

      Рівняння $\frac{{f(x)}}{{g(x)}} = 0$ є рівносильним системі рівнянь 

$\left\{ \begin{array}{l}f(x) = 0,\\g(x) \ne 0.\end{array} \right.$

    Приклад 1. Розв’яжіть рівняння $\frac{{{x^2} + 4x + 3}}{{{x^2} + 2x + 1}} = 0$.

Розв’язання

$\frac{{{x^2} + 4x + 3}}{{{x^2} + 2x + 1}} = 0;\quad \left\{ \begin{array}{l}{x^2} + 4x + 3 = 0,\\{x^2} + 2x + 1 \ne 0;\end{array} \right.\quad \left\{ \begin{array}{l}x = - 3,x = - 1,\\x \ne - 1.\end{array} \right.$

     Отже, х=-3.

     Відповідь: -3.

     Рівняння f(x)=g(x) називається раціональним, якщо f(x) і g(x) – раціональні вирази.

     Щоб розв’язати раціональне рівняння, потрібно:

1. знайти спільний знаменник усіх дробів, що входять до рівняння;

2. замінити дане рівняння цілим, помноживши обидві його частини на спільний знаменник;

3. розв’язати одержане ціле рівняння;

4. виключити з коренів цілого рівняння ті, які перетворюють на нуль спільний знаменник.

    Приклад 2. Розв’яжіть рівняння $1 + \frac{2}{{x - 1}} - \frac{6}{{{x^2} - 1}} = \frac{3}{{x + 1}}$.

Розв’язання

$1 + \frac{2}{{x - 1}} - \frac{6}{{{x^2} - 1}} = \frac{3}{{x + 1}};1 \cdot ({x^2} - 1) + \frac{2}{{x - 1}} \cdot \frac{{{x^2} - 1}}{1} - \frac{6}{{{x^2} - 1}} \cdot \frac{{{x^2} - 1}}{1} = \frac{3}{{x + 1}} \cdot \frac{{{x^2} - 1}}{1}$;

$\left\{ \begin{array}{l}{x^2} - 1 + 2(x + 1) - 6 = 3(x + 1),\\{x^2} - 1 \ne 0;\end{array} \right.\left\{ \begin{array}{l}{x^2} - 7 + 2x + 2 = 3x - 3,\\{x^2} \ne 1;\end{array} \right.\left\{ \begin{array}{l}x2 - x - 2 = 0,\\x \ne \pm 1;\end{array} \right.$

$\left\{ \begin{array}{l}x = 2,x = - 1,\\x \ne \pm 1.\end{array} \right.$

     Отже, х=2.

     Відповідь: 2.

     Нерівність $\frac{{f(x)}}{{g(x)}} > 0$ рівносильна двом системам 

$\left\{ \begin{array}{l}f(x) > 0,\\g(x) > 0\end{array} \right.\quad abo\quad \left\{ \begin{array}{l}f(x) < 0,\\g(x) < 0.\end{array} \right.$

     Нерівність $\frac{{f(x)}}{{g(x)}} < 0$ рівносильна двом системам 

$\left\{ \begin{array}{l}f(x) > 0,\\g(x) < 0\end{array} \right.\quad abo\quad \left\{ \begin{array}{l}f(x) < 0,\\g(x) < 0.\end{array} \right.$

     Нерівність $\frac{{f(x)}}{{g(x)}} \ge 0$ рівносильна двом системам 

$\left\{ \begin{array}{l}f(x) \ge 0,\\g(x) > 0\end{array} \right.\quad abo\quad \left\{ \begin{array}{l}f(x) \le 0,\\g(x) < 0.\end{array} \right.$

     Нерівність $\frac{{f(x)}}{{g(x)}} \le 0$ рівносильна двом системам 

$\left\{ \begin{array}{l}f(x) \ge 0,\\g(x) < 0\end{array} \right.\quad abo\quad \left\{ \begin{array}{l}f(x) \le 0,\\g(x) > 0.\end{array} \right.$

    Приклад 3. Розв’яжіть нерівність $\frac{{x - 2}}{{x - 7}} > 0$.

Розв’язання

$\frac{{x - 2}}{{x - 7}} > 0;\;\left\{ \begin{array}{l}x - 2 > 0,\\x - 7 > 0\end{array} \right.\;abo\;\left\{ \begin{array}{l}x - 2 < 0,\\x - 7 < 0;\end{array} \right.\;todi\;\left\{ \begin{array}{l}x > 2,\\x > 7\end{array} \right.\;abo\;\left\{ \begin{array}{l}x < 2,\\x < 7.\end{array} \right.$

     Звідси $x \in (7; + \infty )$ або $x \in ( - \infty ;2)$.

     Отже. $x \in ( - \infty ;2) \cup (7; + \infty )$.

     Відповідь: $( - \infty ;2) \cup (7; + \infty )$.

Розв’язування раціональних нерівностей методом інтервалів

     Щоб розв’язати нерівність f(x)>0 (f(x)<0, f(x)≥0, f(x)≤0), де $f(x) = \frac{{(x - {a_1})(x - {a_2})...(x - {a_m})}}{{(x - {a_{m + 1}})(x - {a_{m + 2}})...(x - {a_{m + n}})}}$, треба:

1. зобразити числа ${a_1},{a_2},...,{a_n}$  на числовій прямій (ці числа розташовані в порядку зростання і поділяють числову пряму на декілька проміжків, на яких функція f(x) зберігає свій знак, тобто якщо ${a_i},{a_k}$  - сусідні точки, то для $x \in ({a_i};{a_k})$  функція зберігає знак);

2. визначити знаки функції f(x) на кожному з проміжків;

3. записати відповідь, ураховуючи знак нерівності, даної в умові.

    Приклад 4. Розв’яжіть нерівність $\frac{{(x + 4)(x - 1)}}{{(x + 2)(x - 3)}} < 0$.

Розв’язання

     Позначимо на числовій прямій точки: х=-4, х=-2, х=1, х=3 та знайдемо знак функції $f(x) = \frac{{(x + 4)(x - 1)}}{{(x + 2)(x - 3)}}$ на кожному проміжку.

     Відповідь: $( - 4; - 2) \cup (1;3)$.

     Використовується для розв’язування нерівностей f(x)>0 (f(x)<0, f(x)≥0, f(x)≤0). Метод ґрунтується на тому, що неперервна на проміжку функція може змінювати знак тільки в тих точках, де її значення дорівнює нулю (але може й не змінювати).

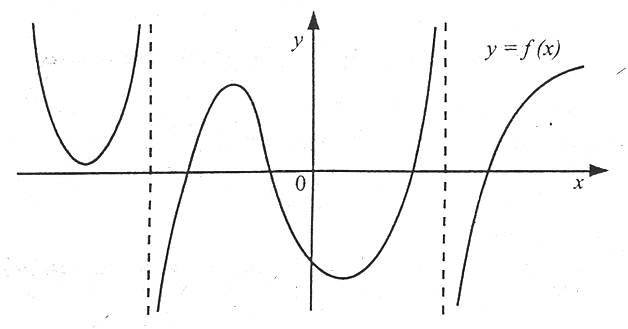
     Щоб розв’язати нерівність методом інтервалів, потрібно:

1. знайти область визначення функції y=f(x);

2. знайти значення х, при яких функція дорівнює нулю (знайти всі нулі функції): f(x)=0;

3. розбити область визначення на проміжки, у яких кожен із кінців є коренем рівняння f(x)=0 або кінцевою точкою проміжку визначення функції y=f(x);

4. визначити знак f(x) на кожному з утворених проміжків;

5. об’єднати проміжки, на яких функція f(x) задовольняє нерівність, у множину розв’язків.

    Приклад 5. Розв’яжіть нерівність $\frac{{{x^2} - 2x - 3}}{{{x^2} + 3x - 4}} \ge 0$.

Розв’язання

     Розкладемо чисельник і знаменник дробу на множники й одержимо

$\frac{{(x - 3)(x + 1)}}{{(x - 1)(x + 4)}} \ge 0$.

     Позначимо на силовій прямій точки 3; -1; 1; -4, у яких чисельник або знаменник дробу перетворюється на нуль. Ці точки поділяють числову пряму на п’ять проміжків. При х>3 усі множники чисельника і знаменника дробу додатні, то дріб є додатним.

     При переході від одного проміжку до іншого дріб змінює знак, тому можна розставити знаки. Значення х=-1, х=3 задовольняють дану нерівність, а при х=1, х=-4 дріб не має змісту. Таким чином дана нерівність має розв’язок $( - \infty ; - 4) \cup [ - 1;1) \cup [3; + \infty )$.

     Відповідь: $( - \infty ; - 4) \cup [ - 1;1) \cup [3; + \infty )$.