Показникова функція. Показникові рівняння, нерівності та їх системи
Показникова функція. Показникові рівняння, нерівності та їх системи
| Сайт: | Підготовка до ЗНО - Освітній портал "Академія" |
| Курс: | Підготовка до ЗНО з математики. Алгебра. |
| Книга: | Показникова функція. Показникові рівняння, нерівності та їх системи |
| Надруковано: | Гість |
| Дата: | Wednesday 2 July 2025 8:07 AM |
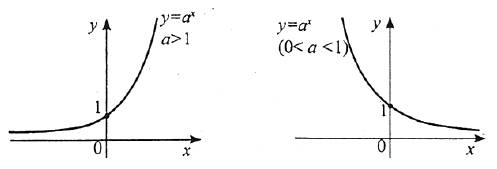
1. Показникова функція
Функцію виду  називають показниковою.
називають показниковою.
Основні властивості
- Область визначення – множина всіх дійсних чисел R.
- Область значень – (0;+∞).
- Якщо х=0, то у=1.
- Функція не є ні парною, ні не парною.
- Якщо а>1, тоді функція
 зростає; якщо 0<а<1, то функція спадає.
зростає; якщо 0<а<1, то функція спадає. - При а>1 і х>1,
 ; при х<0,
; при х<0,  . При 0<а<1
. При 0<а<1  , якщо х>0;
, якщо х>0;  при х<0.
при х<0. - Графік функції

2. Показникові рівняння
Показниковими називаються рівняння, в яких невідоме міститься в показнику степеня при сталих основах.
Наприклад: рівняння  є показниковими.
є показниковими.
Найпростішим показниковими рівнянням є рівняння  .
.
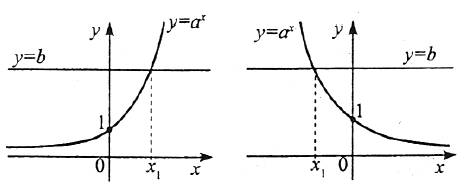
Оскільки множина значень функції  - множина додатних чисел, то рівняння
- множина додатних чисел, то рівняння  :
:
1) має один корінь, якщо b>0;
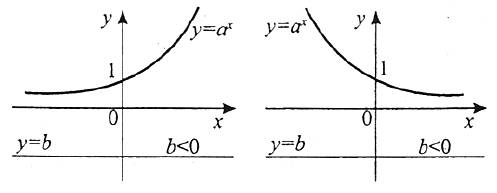
2) не має коренів, якщо b≤0.
Для того, щоб розв’язати рівняння  , треба b подати у вигляді
, треба b подати у вигляді  , тобі будемо мати
, тобі будемо мати  , звідси х=с.
, звідси х=с.
Розглянемо приклади.
Приклад 1. Розв’яжіть рівняння .
Розв’язання
Оскільки  , а
, а  , то маємо
, то маємо  , звідси х=3.
, звідси х=3.
Відповідь: 3.
Приклад 2. Розв’яжіть рівняння  .
.
Розв’язання
Оскільки  , то маємо
, то маємо  , звідси х=-2.
, звідси х=-2.
Відповідь: -2.
Приклад 3. Розв’яжіть рівняння  .
.
Розв’язання
Оскільки  , то
, то  , звідси х1=2, х2=3.
, звідси х1=2, х2=3.
Відповідь: 2; 3.
3. Деякі способи розв’язування показникових рівнянь
І спосіб. Приведення рівняння до спільної основи, тобто до рівняння  .
.
Як відомо, показникова функція  монотонна, тому кожне своє значення вона приймає тільки при одному значенні аргументу. Із рівності випливає, що f(x)=g(x).
монотонна, тому кожне своє значення вона приймає тільки при одному значенні аргументу. Із рівності випливає, що f(x)=g(x).
ІІ спосіб. Винесення спільного множника за дужки.
ІІІ спосіб. Приведення рівняння до квадратного.
IV спосіб. Графічний спосіб роз взування показникових рівнянь.
Приклад 1. Розв’яжіть графічно рівняння  .
.
Розв’язання
Побудуємо графіки функцій  в одній системі координат. Графіки функцій
в одній системі координат. Графіки функцій  і
і  перетинаються в точці, абсциса якої х=0.
перетинаються в точці, абсциса якої х=0.
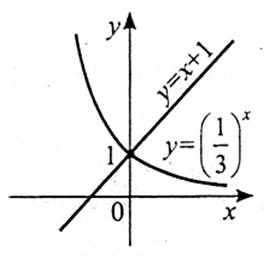
Відповідь: 0.
Зауваження. Корінь цього рівняння легко знайти усно, однак треба пам’ятати, що в цьому випадку необхідно доводити той факт, що знайдений корінь єдиний.
4. Системи показникових рівнянь
При розв’язуванні систем показникових рівнянь використовуються традиційні способи розв’язування показникових рівнянь і знайомі Вам способи розв’язування систем рівнянь.
Приклад 1. Розв’яжіть систему рівнянь
Розв’язання
Зробимо заміну  , тоді матимемо систему:
, тоді матимемо систему:
Розв’яжемо систему рівнянь:
Отже,
Відповідь: (2;1).
5. Показникові нерівності
Розв’язування показникових нерівностей часто зводяться до розв’язування нерівностей  або
або  . Ці нерівності розв’язують, використовуючи монотонність (зростання, спадання) показникової функції.
. Ці нерівності розв’язують, використовуючи монотонність (зростання, спадання) показникової функції.
Розглянемо приклади.
Приклад 1. Розв’яжіть нерівність  .
.
Розв’язання
Запишемо дану нерівність у вигляді  . Оскільки 3>1, то функція
. Оскільки 3>1, то функція  є зростаючою. Отже, при х<3 виконується нерівність
є зростаючою. Отже, при х<3 виконується нерівність  .
.
Відповідь: (-∞;3).
Приклад 2. Розв’яжіть нерівність  .
.
Розв’язання
Запишемо дану нерівність у вигляді  . Оскільки
. Оскільки  – спадна функція, то
– спадна функція, то  .
.




