Логарифми. Логарифмічна функція. Логарифмічні рівняння, нерівності та їх системи

     Означення логарифма можна коротко записати так:

${a^{{{\log }_a}b}} = b$.

     Ця рівність справедлива при b>0, a>0, a≠0 і називається основною логарифмічною тотожністю.

     Наприклад: ${2^{{{\log }_2}5}} = 5;\;{2^{ - {{\log }_2}5}} = {({2^{{{\log }_2}5}})^{ - 1}} = \frac{1}{5}$.

Основні властивості логарифмів

     При виконанні перетворень виразів, які містять логарифми, при обчисленнях і при розв’язуванні рівнянь, нерівностей часто використовуються властивості логарифмів.

     Для будь-яких а>0, а≠1 і будь-яких додатних х і у виконуються такі рівності:

1. ${\log _a}1 = 0$;
2. ${\log _a}a = 1$;
3. ${\log _a}xy = {\log _a}x + {\log _a}y$;
4. ${\log _a}\frac{x}{y} = {\log _a}x - {\log _a}y$;
5. ${\log _a}{x^p} = p{\log _a}x\;(p \in R)$;
6. ${\log _{{a^p}}}x = \frac{1}{p}{\log _a}x\;(p \in R)$;
7. ${\log _a}x = \frac{{{{\log }_b}x}}{{{{\log }_b}a}}\;(b > 0,b \ne 1)$.

     Рівняння ${a^x} = b$, де $a > 0,\;a \ne 1,\;b > 0$, має єдиний корінь. Його називають логарифмом числа b з основою а і позначають ${\log _a}b$.

     Наприклад: коренем рівняння ${2^x} = 8$ є число 3, тобто ${\log _2}8 = 3$.

     Логарифмом додатного числа b за основою а, де а>0, а≠1, називають показник степеня, до якого треба піднести число а, щоб одержати число b.

     Наприклад: ${\log _2}8 = 3$, оскільки ${2^3} = 8$;

${\log _2}\frac{1}{4} = - 2$, оскільки ${2^{ - 2}} = \frac{1}{4}$;

${\log _7}1 = 0$, оскільки ${7^0} = 1$.

     Розглянемо приклади використання формул 3 – 7. Обчислимо:

1)               ${\log _6}18 + {\log _6}2 = {\log _6}(18 \cdot 2) = {\log _6}36 = 2$;

2)               ${\log _{12}}48 - {\log _{12}}4 = {\log _{12}}\frac{{48}}{{12}} = {\log _{12}}12 = 1$;

3)               ${\log _3}\sqrt 3 = {\log _3}{3^{\frac{1}{2}}} = \frac{1}{2}{\log _3}3 = \frac{1}{2} \cdot 1 = \frac{1}{2}$;

4)               ${\log _{125}}5 = {\log _{{5^3}}}5 = \frac{1}{3}{\log _5}5 = \frac{1}{3} \cdot 1 = \frac{1}{3}$;

5)               $\frac{{{{\log }_3}16}}{{{{\log }_3}4}} = {\log _4}16 = {\log _4}{4^2} = 2{\log _4}4 = 2 \cdot 1 = 2$.

     Формулу 7 називають формулою переходу до логарифмів з іншою основою.

     За допомогою формули 7 можна знаходити логарифми з довільною основою а, маючи таблиці логарифмів, складених для якої-небудь основи b. Найбільш уживаними є таблиці десяткових і натуральних логарифмів.

     Десятковими логарифмами називають логарифми за основою 10, позначають lg.

     Наприклад: $\lg 100 = 2;\;\lg 0,0001 = - 4$.

     Натуральними логарифмами називають логарифми за основою е (число е – ірраціональне, е≈2,718…), позначають ln.

     Наприклад: $\ln e = 1;\;\ln {e^2} = 2;\;\ln \frac{1}{e} = - 1$.

     Дію знаходження логарифма числа (виразу) називають логарифмуванням.

     Приклад 1. Прологарифмувати вираз $y = \frac{{{a^2}{b^2}}}{{{c^3}}}$.

Розв’язання

$\lg y = \lg \frac{{{a^2}{b^2}}}{{{c^3}}} = \lg ({a^2}{b^2}) - \lg {c^3} = \lg {a^2} + \lg {b^2} - \lg {c^3} = 2\lg a + 2\lg b + 3\lg c$.

     Дію, обернену до логарифмування, називають потенціюванням.

     Потенціювання – знаходження числа (виразу) за його логарифмом.

     Приклад 2. Пропотенціювати вираз $\lg x = \frac{1}{2}\lg 5a - 3\lg b + 4\lg c$.

Розв’язання

$\lg x = \frac{1}{2}\lg 5a - 3\lg b + 4\lg c;\;\lg x = \lg {(5a)^{\frac{1}{2}}} - \lg {b^3} + \lg {c^4}$;

$\lg x = \lg \sqrt {5a} - \lg {b^3} + \lg {c^4};\;\lg x = \lg (\sqrt {5a} \cdot {c^4}) - \lg {b^3}$;

$\lg x = \lg \frac{{{c^4}\sqrt {5a} }}{{{b^3}}};\;x = \frac{{{c^4}\sqrt {5a} }}{{{b^3}}}$.

     Функцію виду $y = {\log _a}x$, де $a > 0,\;a \ne 1$, називають логарифмічною.

     Основні властивості логарифмічної функції

1. Область визначення – (0;+∞).
2. Область значень – множина всіх дійсних чисел R.
3. Якщо х=1, то у=0.
4. Функція $y = {\log _a}x$ не є ні парною, ні непарною.
5. Якщо а>1, функція $y = {\log _a}x$ зростає, а при 0<а<1 – спадає.
6. Якщо а>1 і х>1, то $y = {\log _a}x > 0$. Якщо а>1 і 0<х<1, то $y = {\log _a}x < 0$. Якщо 0<а<1 і х>1, то $y = {\log _a}x < 0$. Якщо 0<а<1 і 0<х<1, то $y = {\log _a}x > 0$.
7. Графік функції $y = {\log _a}x$:

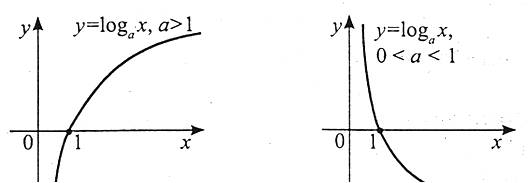
     При знаходженні області визначення слід пам’ятати:

1)               Якщо функція має вигляд $y = {\log _a}(f(x)),a > 1,a \ne 1$, то слід вважати f(x)>0 (під знаком логарифма може стояти тільки додатний вираз).

     Наприклад: якщо $y = \lg ({x^2} - 5x + 6)$, то ${x^2} - 5x + 6 > 0$, тобто $D(y) = ( - \infty ;2) \cup (3; + \infty )$.

2)               Якщо функція має вигляд $y = {\log _{f(x)}}b,b > 0$, то слід вважати

$\left\{ \begin{array}{l}f(x) > 0,\\f(x) \ne 1\end{array} \right.$

 (основа логарифма може бути тільки додатною і відмінною від одиниці).

     Наприклад: якщо $y = {\log _{x - 1}}10$, то 

$\left\{ \begin{array}{l}x - 1 > 0,\\x - 1 \ne 1,\end{array} \right.$

тобто $D(y) = (1;2) \cup (2; + \infty )$.

     Логарифмічними називають рівняння, які містять змінну під знаком логарифма.

     Приклад 1. Логарифмічні рівняння: 

$\lg x = 1 + {\lg ^2}x,\;{\log _2}(x + 3) = 9,\;\sqrt {\lg x} = \lg \sqrt x$.

     Розв’язати логарифмічне рівняння – це означає знайти всі його корені або довести, що рівняння коренів не має.

     Найпростіше логарифмічне рівняння має вигляд ${\log _a}x = b$, де $a > 0,a \ne 1,x > 0$. З означення логарифма випливає, що $x = {a^b}$.

     Інший вигляд найпростішого логарифмічного рівняння:

${\log _a}x = {\log _a}b$, де $a > 0,a \ne 1,x > 0,b > 0$.

     Із цього рівняння випливає, що х=b. Дійсно із рівності  на підставі означення логарифма і логарифмічної тотожності маємо

$x = {a^{{{\log }_a}b}} = b$.

     Найпростішим логарифмічним рівнянням є рівняння

${\log _a}x = b$, де $x > 0,x \ne 1,a > 0$.

      За означенням логарифма маємо

${x^b} = a$, звідси $x = {a^{\frac{1}{2}}}$.

     В основному, усі логарифмічні рівняння зводяться до розв’язування найпростіших рівнянь.

     Зазначимо, що в прикладах використовуються тільки такі перетворення, які не призводять до втрати коренів, але можуть привести до одержання сторонніх коренів. Тому перевірка кожного з одержаних коренів обов’язкова, якщо немає впевненості у рівносильності рівнянь.

Основні методи розв’язування логарифмічних рівнянь

1. Метод зведення логарифмічного рівняння до алгебрагічного.

2. Метод потенціювання.

3. Метод зведення логарифмів до однієї основи.

4. Метод логарифмування.

5. Графічний метод розв’язування логарифмічних рівнянь.

     При розв’язуванні систем логарифмічних рівнянь використовують такі самі способи, що й при розв’язуванні алгебраїчних систем.

     Завдання. Розв’яжіть систему рівнянь 

$\left\{ \begin{array}{l}\lg x - \lg y = 7,\\\lg x + \lg y = 5.\end{array} \right.$

Розв’язання

     Додамо і віднімемо почленно рівняння системи, тоді одержимо:

$\left\{ \begin{array}{l}2\lg x = 12,\\ - 2\lg y = 2;\end{array} \right.\;\left\{ \begin{array}{l}\lg x = 6,\\\lg y = - 1;\end{array} \right.\;\left\{ \begin{array}{l}x = {10^6},\\y = {10^{ - 1}}.\end{array} \right.$

Відповідь: $({10^6};{10^{ - 1}})$.

Як відомо, логарифмічна функція $y = {\log _a}x$ зростає при а>1, спадає – при 0<а<1. Зі зростанням функції $y = {\log _a}x$ у першому випадку і спадання – у другому випливає:

1)               При а>1 нерівність ${\log _a}{x_2} > {\log _a}{x_1}$ рівносильна системі 

$\left\{ \begin{array}{l}{x_2} > {x_1},\\{x_1} > 0,\\{x_2} > 0.\end{array} \right.$

2)               При 0<а<1 нерівність ${\log _a}{x_2} > {\log _a}{x_1}$ рівносильна системі 

$\left\{ \begin{array}{l}{x_2} < {x_1},\\{x_1} > 0,\\{x_2} > 0.\end{array} \right.$

     Як правило, логарифмічна нерівність зводиться до нерівностей виду ${\log _a}f(x) > {\log _a}g(x)$, де $a > 0,a \ne 1$.

     Якщо а>1, то нерівність ${\log _a}f(x) > {\log _a}g(x)$ рівносильна системі нерівностей 

$\left\{ \begin{array}{l}f(x) > 0,\\g(x) > 0,\\f(x) > g(x).\end{array} \right.$

     Якщо 0<а<1, то нерівність ${\log _a}f(x) > {\log _a}g(x)$ рівносильна системі нерівностей 

$\left\{ \begin{array}{l}f(x) > 0,\\g(x) > 0,\\f(x) < g(x).\end{array} \right.$