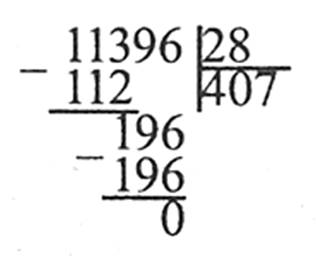Підготовка до ЗНО з математики. Алгебра.

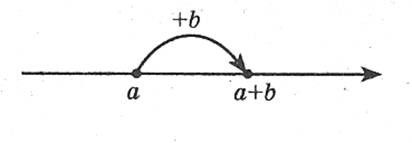
Додавання натуральних чисел

Наприклад: 5 + 3 = 5 + 1 + 1 + 1 = 8.

Додавання багатоцифрових натуральних чисел виконується порозрядно (додавання одноцифрових чисел кожного стовпчика, починаючи з правого стовпчика).

Наприклад:

362 + 473 = 835;

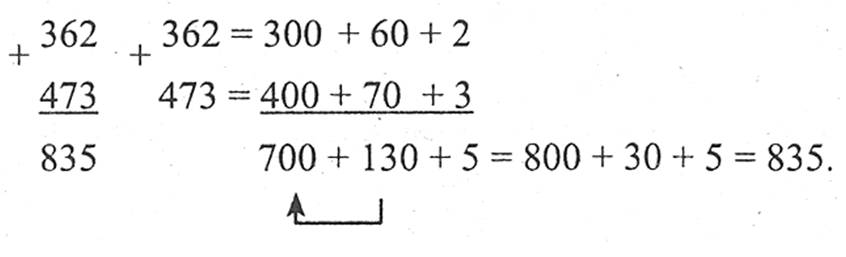
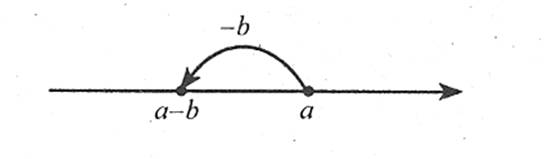
Віднімання натуральних чисел

Відняти від числа a число b означає знайти таке число с, що a = b + с.

Наприклад: 10 – 3 = 10 – 1 – 1 – 1 = 7.

Віднімання багатоцифрових натуральних чисел виконується порозрядно (віднімання одноцифрових чисел кожного стовпчика, починаючи з правого стовпчика).

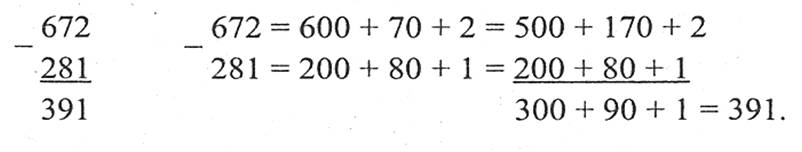
Множення натуральних чисел

Наприклад: 2 ˑ 3 = 2 + 2 + 2 = 6.

Множення багатоцифрових натуральних чисел виконується «у стовпчик».

Наприклад: 459ˑ275=126225.

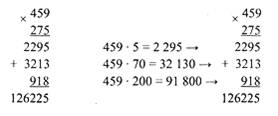
Ділення натуральних чисел

Розділити число a на число b означає знайти таке число с, що a = b ˑ с.

Натуральне число a розділити на натуральне число b означає підрахувати, скільки разів треба відняти число b від числа a, щоб одержати нуль.

Наприклад: 6 : 3 = 2, бо 6 – 3 – 3 = 0.

Ділення натуральних чисел з остачею

Якщо a ― ділене, b ― дільник і a = bс + r, де b > r, то говорять, що при діленні числа a на число b маємо неповну частку с та остачу r:

.

Наприклад: 10 : 4 = 2 (остача 2), 10 = 4 · 2 + 2.

Ділення багатоцифрових чисел виконується «кутом».

Наприклад:

113 сотень: 28 = 4 сотні (остача 1 сотня);

19 десятків: 28 = 0 десятків (остача 19 десятків);

196 : 28 = 7.