Підготовка до ЗНО з математики. Геометрія.

     Геометрія вивчає властивості фігур, які виражаються різними твердженнями: означеннями, аксіомами, теоремами.

     Означення – це твердження, яке пояснює дане поняття через уже відомі поняття.

     Аксіома – це твердження, яке приймається на віру (без доведення).

    Наприклад:

1. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй.

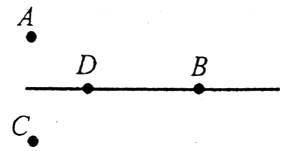
2. Через будь-які дві точки можна провести пряму, і тільки одну.

3. Пряма розбиває площину на дві півплощини.

4. Із трьох точок прямої одна і тільки одна лежить між двома іншими.

     Теоремою називається твердження про властивість фігури, істинність якого встановлюється у результаті міркувань. Ці міркування називаються доведенням.

     Наведемо приклад.

    Теорема. Дві різні прямі можуть перетинатися тільки в одній точці.

Доведення

     Якби дві різні прямі мали дві точки перетину, то через ці точки проходили б дві різні прямі. А це неможливо, оскільки через дві різні точки можна провести тільки одну пряму (аксіома 2). Отже, дві різні прямі не можуть мати дві різні точки перетину.