Підготовка до ЗНО з математики. Геометрія.

     Дві прямі на площині можуть мати спільну точку або не мати спільних точок. Дві прямі, які мають спільну точку, називаються прямими, що перетинаються.

    Означення. Дві прямі, які лежать в одній площині і не перетинаються, називаються паралельними.

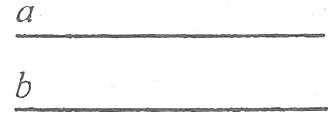
     Паралельність прямих позначається знаком . Паралельність прямих а і b записується так:  .

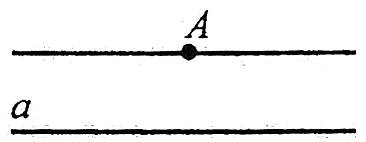
     Аксіома паралельних прямих

     Через точку, яка не лежить на даній прямій, можна провести в площині єдину пряму, паралельну даній прямій.

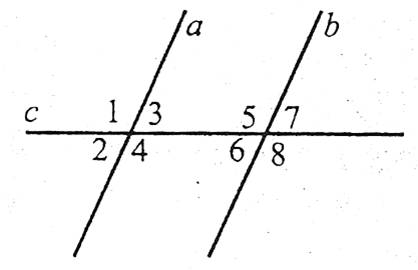
     Нехай прямі а і b перетинаються третьою прямою с, яка називається січною. Тоді утворюється вісім кутів, які мають спеціальні назви: кути 3, 4, 5, 6 – внутрішні, кути 1, 2, 7, 8 – зовнішні.

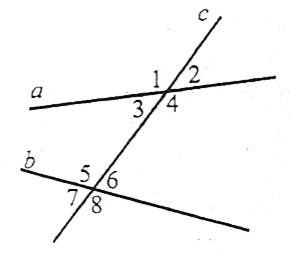
     Пари кутів 1 і 5, 2 і 6, 3 і 7, 4 і 8 називаються відповідними, пари кутів 3 і 6, 4 і 5 – внутрішніми різносторонніми, пари кутів 1 і 8, 2 і 7 – зовнішніми різносторонніми. Пари кутів 3 і 5, 4 і 6 називаються, 1 і 7, 2 і 8 – зовнішніми односторонніми.

     Якщо дві паралельні прямі а і b перетнуті прямою с, то:

1. внутрішні різносторонні кути ріні, тобто ;
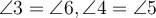2. сума внутрішніх односторонніх кутів дорівнює 180°, тобто , ;
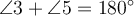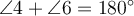3. відповідні кути рівні, тобто ;
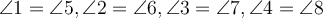4. зовнішні різносторонні кути рівні, тобто ;
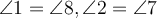5. сума зовнішніх односторонніх кутів дорівнює 180°, тобто .
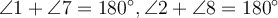